Hintergrund

Streichholzvierlinge – eine Gute Aufgabe

Wenn Sie sich die Aufgaben in Ihren Mathematikschulbüchern ansehen, dann haben Sie sich sicherlich schon häufiger gefragt, ob diese Aufgabe oder diese Seite wirklich sinnvoll sind. Die Entscheidung eine Aufgabe wegzulassen wird häufig intuitiv gefällt. Aber gibt es auch didaktisch begründete Kriterien, die einem helfen, Aufgaben als Gute Aufgaben zu erkennen, oder aus einer nicht so Guten Aufgabe, eine gute zu machen?
Anhand der Streichholzvierlinge sollen die Kriterien Guter Aufgaben vorgestellt und erörtert werden.

Damit Sie darauf aufbauend guten Unterricht vorbereiten können, nehmen wir nun Folgendes in den Blick:

• Streichholzvierlinge - Vorstellen des Aufgabenformats
• Kriterien für gute Aufgaben
• Streichholzvierlinge - Eine gute Aufgabe?
• Aufgaben variieren - Aus einer guten Aufgabe weitere gute Aufgaben machen

Was sind Streichholz-Vierlinge

Streichholzvierling bestehen – wie der Name schon sagt – aus immer vier Hölzern (am besten nimmt man keine echten Streichhölzer, sondern Hölzer ohne Zündkopf, die es als Bastelmaterial zu kaufen gibt).
Diese müssen entweder gradlinig oder im rechten Winkel aneinandergelegt werden. Nachfolgend sehen Sie einige Beispiele:

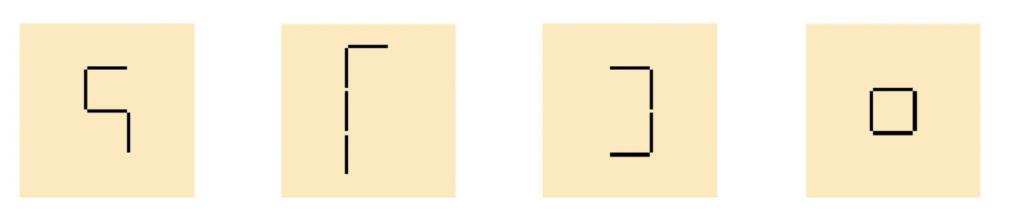
Dabei gilt immer die Regel, dass gespiegelte Vierlinge als verschieden angesehen werden. Können die Vierlinge durch Drehungen ineinander übergeführt werden, gelten sie aber als gleich.

Eigenaktivität

Überlegen Sie, welche der untenstehenden Streichholzvierlinge gleich sind.

Kommentar zur Eigenaktivität

2 und 3 sind gleich, 1 ist das Spiegelbild von 2 und 3

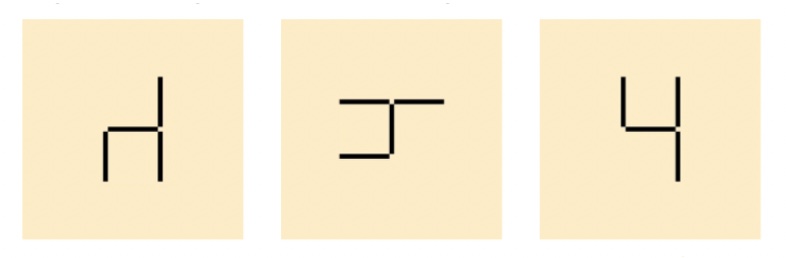
Eigenaktivität

Nehmen Sie sich vier Streichhölzer oder auch nur Zettel und Stift und versuchen Sie möglichst alle Vierlinge zu finden. Wie sind Sie vorgegangen? Wie viele haben Sie gefunden?

Kommentar zur Eigenaktivität

Wenn Sie auf die nebenstehende Abbildung klicken, werden Ihnen alle Streichholzvierlinge in vergrößerter Form angezeigt.

Was sind gute Aufgaben?

Wie bereits auf der Seite Unterricht, mehr als gute Aufgaben erwähnt, wird in den Handreichungen zu den Bildungsstandards konkretisiert, welche Kriterien Gute Aufgabe zu erfüllen haben (MSW NRW 2008, S. 13f.):
„Gute Lernaufgaben

• fordern und fördern inhalts- und prozessbezogene so wie übergreifende Kompetenzen
• sind herausfordernd auf unterschiedlichem Anspruchsniveau
• knüpfen an Vorwissen an und bauen das zu erwerbende Wissen kumulativ (vernetzt) auf
• sind in sinnstiftende Kontexte eingebunden
• sind vielfältig in den Lösungsstrategien und Darstellungsformen
• stärken das Könnensbewusstsein durch erfolgreiches Bearbeiten.“

Diese Auflistung stellt natürlich erstmal nur eine grobe Orientierung dar, ist aber sicherlich recht unkonkret, wenn man z.B. eine Schulbuchaufgabe oder -seite mit diesen Charakterisierungen analysieren will. Festzustellen ist, dass Gute Aufgaben im Kern ermöglichen wollen, dass die Kinder an einem gemeinsamen Gegenstand, in Kooperation miteinander, zugleich aber auf ihrem jeweiligen Entwicklungsniveau und mittels ihrer grundsätzlich gegenwärtigen und augenblicklich aktivierten Denk- und Handlungskompetenzen lernen können.
Das zentrale Ziel einer „guten Aufgabe“ ist somit die Entwicklung sowohl inhalts- als auch prozessbezogener Kompetenzen auf dem jeweiligen Niveau des Kindes. Dies verdeutlicht, warum eine Analyse von Aufgaben vor dem Hintergrund der obigen Charakterisierungen schwer erscheint.
Schließlich entfaltet eine Gute Aufgabe erst ihr gesamtes Potential, wenn sie unterrichtlich entsprechend eingebunden wird.
Denn: Gute Aufgaben sind nicht per se Gute Aufgabe, erst der Unterricht macht sie dazu!
Damit diese ihre Wirksamkeit auch wirklich entfalten können, ist eine entsprechend lernfördernde Unterrichtsgestaltung unumgänglich. Denn Aufgaben- und Unterrichtsqualität bedingen sich gegenseitig.
So stellen sich schnell Fragen wie die folgenden: Was muss die Lehrperson initiieren, damit z.B. …

• inhalts- und prozessbezogene Kompetenzen angesprochen werden?
• die Problemstellung für die Kinder wirklich sinnstiftend und herausfordernd ist?
• die Aufgabenstellung zu entdeckendem Lernen anregt (und die Kinder auch wirklich Gehaltvolles entdecken und nutzen)?
• die Kinder weitgehend selbstständig auf unterschiedlichem Niveau arbeiten können?
• die Kinder zu ergiebigen Reflexionen ihrer Vorgehensweisen und Strategien angeregt werden und die Lernerfahrungen bewusst gemacht werden?
• die Kinder einen tatsächlichen Lernzuwachs hinsichtlich ihrer non-verbalen und verbalen Darstellungsfähigkeit erzielen?
• der Austausch über Lösungswege kooperativ, strukturiert und ergiebig erfolgt?

​Zur Entfaltung einer Guten Aufgabe muss somit auch eine gute unterrichtliche Einbettung dieser Aufgabe stattfinden. Erst in einem Unterricht, der den Kindern den Freiraum gibt, eigene Wege gehen zu dürfen, Strategien gemeinsam zu besprechen, das Lernen von- und miteinander zu ermöglichen, ... Es ist ein Unterricht, der eben nicht vom Lehrervortrag oder individueller Einzelarbeit (z.B. durch das Durcharbeiten von Heften oder Abarbeiten von Schulbuchseiten in individuellem Tempo) geprägt ist. Es ist vielmehr ein Unterricht, der von der Diskussion und Kommunikation unter den Kindern lebt.
Eine Lehrkraft muss sich daher inhaltlich mit der Aufgabe auseinandergesetzt haben, damit man dieses Potential für eine unterrichtliche Umsetzung überhaupt wahrnimmt.

Gute Aufgaben - Guter Unterricht

Guter Unterricht bedarf Guter Aufgaben. Gute Mathematikaufgaben sind jedoch umgekehrt noch keine Garantie für einen guten Mathematikunterricht. Entscheidend sind der Umgang des Lehrers und der Schüler mit den Aufgaben. Um das Aufgabenangebot in offenen Lernsituationen effektiv zu nutzen und kompetenzorientiert zu bewältigen, bedürfen Kinder besonderer Hilfen und Unterstützungsmaßnahmen (z.B. über Forschermittel, vgl. PIKAS: Unterrichtsmodul: 'Gute Aufgaben- Forschermittel-Plakat').
In der Funktion eines Lernbegleiters unterstützt die Lehrkraft die Kinder dabei, ihre Arbeit selbstständig zu organisieren und zu strukturieren. Sie beobachtet das individuelle Lernen der Kinder, gibt weiterführende Impulse und berät bei der Auswahl differenzierter Teilaufgaben. Sie bahnt Gruppenprozesse an und organisiert einen ergiebigen, strukturierten Austausch der Kinder untereinander (vgl. MSW NRW 2008, S. 14).
Das Wechselspiel zwischen Art der Aufgabenstellung und der Gestaltung des Unterrichts sind entscheidend für die Entwicklung fachbezogener Kompetenzen. Viele Anregung zum Umsetzung guter Aufgabe in einem guten Unterricht finden Sie bei unserem Partnerprojekt PIKAS: Unterrichtsmodul: 'Gute Aufgaben - Unterrichtsmaterial'.

Warum ist das Finden aller Streichholzvierlinge eine Gute Aufgabe?

Im Folgenden gehen wir alle Kriterien für Gute Aufgabe durch und überlegen, ob diese mit dem Arbeitsauftrag „Findet möglichst viele Streichholzvierlinge!“ erfüllt werden können.
Überlegen Sie dazu für jedes Kriterium, ob und unter welchen Bedingungen dieses erfüllt wird oder nicht.

• Es werden inhalts- und prozessbezogene Kompetenzen gefördert und gefordert.
  Beim Finden aller Vierlinge üben die Kinder ihre Raumwahrnehmung, denn sie müssen gleiche Vierlinge als gleich erkennen (auch in gedrehter Position) und von gespiegelten unterscheiden. Vor allem schulen sie aber prozessbezogene Kompetenzen.
  So gehen sie möglicherweise anfangs noch unsystematisch vor und überlegen sich dann eine Systematik, wie sie geschickt weitere Vierlinge finden. So werden z.B. Spiegelbilder sofort mitgelegt oder nur einzelne Streichhölzer systematisch versetzt. Sie üben sich daher im Problemlösen. Zudem kommunizieren die Kinder miteinander, stellen ihren Mitschülern z.B. ihre Vorgehensweise vor oder notieren diese in einem Forscherheft. Dabei benutzen sie möglicherweise auch Fachbegriffe wie „rechter Winkel“ oder „geradlinig“. Letztlich sollten sie argumentieren, warum sie wirklich alle möglichen Vierlinge gefunden haben.
• Die Problemstellung ist für die Kinder wirklich sinnstiftend und herausfordernd.
  Herausfordernd ist die Aufgabe alle Vierlinge zu finden auf jeden Fall, denn die Kinder haben zunächst keine Strategien, wie sie systematisch alle 25 Streichholzvierlinge finden müssen. Die Sinnstiftung besteht in einer Motivation, die von diesem Forscherauftrag ausgeht: Die Kinder wollen unbedingt alle Vierlinge finden.
• Die Aufgabenstellung regt zum entdeckenden Lernen an (und die Kinder auch wirklich Gehaltvolles entdecken und nutzen).
  Die Kinder entdecken eigene Herangehensweisen und Strategien, möglichst viele zu finden. Dazu werden z.B. gefundene Vierlinge sortiert und gruppiert, und damit Gemeinsamkeiten und Unterschiede entdeckt.
• Die Kinder können weitgehend selbstständig auf unterschiedlichem Niveau arbeiten.
  Manche Kinder werden nicht alle Vierlinge finden, manche finden alle und können auch begründen, warum es alle sind. Manche Kinder arbeiten mit Material, manche werden sofort viele Vierlinge aufzeichnen und ggf. nur wenig Vierlinge legen müssen.
• Die Kinder werden zu ergiebigen Reflexionen ihrer Vorgehensweisen und Strategien angeregt und die Lernerfahrungen bewusst gemacht.
  In einer DU-Phase können sich z.B. zwei oder drei Kinder zusammensetzen und gefundene Vierlinge vergleichen. In der gemeinschaftlichen Reflexion im Klassenverband (WIR-Phase) können Strategien zum Finden aller Vierlinge besprochen und dabei alle Vierlinge an der Tafel gesammelt werden. Es kann besprochen werden, welche Vierlinge schwer zu finden waren, und woran das lag.
• Die Kinder erzielen einen tatsächlichen Lernzuwachs hinsichtlich ihrer non-verbalen und verbalen Darstellungsfähigkeit.
  Dies ist kein Arbeitsauftrag, der in Stillarbeit bearbeitet wird. Vielmehr müssen die Kinder sich untereinander austauschen, Vierlinge vergleichen, herausfinden ob sie alle gefunden haben, Strategien erklären ... .
• Der Austausch über Lösungswege erfolgt kooperativ, strukturiert und ergiebig.
  Nach der individuellen Einzelarbeit gehen die Kinder zu zweit oder dritt zusammen und vergleichen ihre gefundenen Vierlinge. Gemeinsam überlegen sie, ob sie noch weitere finden. Dazu sortieren sie die Vierlinge und finden gemeinsam Argumente. Diese werden dann in der Reflexionsphase gemeinsam besprochen.

Hier können Sie die Lösung als Datei herunterladen.

Aufgabenvariation

Aus einer einzelnen Guten Aufgabe entsteht schlussendlich noch keine gute Unterrichtsreihe. Es ist daher immer die Frage, wie man aus einer guten Aufgabe, weitere machen kann. Dazu sind sogenannte Aufgabenvariationen notwendig. Darunter sind „variable Bestimmungselemente“ (Walther, van den Heuvel-Panhuizen, Granzer & Köller 2008) einer Aufgabe zu verstehen. Konkret bedeutet dies, dass ich mir als Lehrperson überlegen muss, wie man die Aufgabe leicht verändert, so dass neue (ergänzende oder vertiefende) Kompetenzen an einer parallelen Aufgabe erworben werden können. Für die Streichholzvierlinge könnten das z.B. die folgenden sein:

• Wie viele Streichholzdrillinge gibt es? Wie kannst du die Vierlinge nutzen, um alle Drillinge zu finden?
• Nimm einen Vierling und versuche möglichst viele Fünflinge zu erzeugen? Aus welchen Vierlingen hast du viele Fünflinge bauen können? Aus welchem nur wenige? Woran lag das?
• Spielt das Spiel Vierlino (siehe Unterricht). Besprecht eure Spielstrategien. Wie könnt ihr sehen, ob ihr einen Vierling im Spiel ablegen könnt?
• Löst weitere Arbeitsblätter- und Forscheraufträge zu Vierlino (siehe Unterricht). Wie geht ihr vor, um diese zu lösen?

Viele dieser Aufgabenvariationen werden im Unterrichtsteil konkret umgesetzt.
Bei anderen – nicht geometrischen – Aufgaben sind andere Aufgabenvariationen möglich. Bei unserem Partnerprojekt PIKAS: Unterrichtsmodul: 'Gute Aufgaben' finden Sie viele verschiedene Beispiele guter Aufgaben mit entsprechender Aufgabenvariation.

Diese Seite wurde auf der Grundlage eines Skripts von Tobias Huhmann für das primakom-Team erstellt.