Ebene Figuren
Kinder haben bereits vor Schuleintritt auch im Bereich der Geometrie vielfältige Erfahrungen gesammelt, Vorstellungen entwickelt und Wissen erworben. Diese Vorerfahrungen der Kinder sind zu ergründen, zu nutzen, zu präzisieren und zu erweitern.
Im Geometrieunterricht der Grundschule sind somit grundlegende Kenntnisse über ebene Figuren zu erarbeiten und Fähigkeiten und Fertigkeiten im Operieren mit ebenen Figuren zu entwickeln, die es den Kindern ermöglichen, Beziehungen zwischen ihnen zu erkennen und zu nutzen sowie eine adäquate Sprachkultur zu etablieren.
Auf dieser Seite erhalten Sie Hintergrundinformationen zu folgenden zentralen Fragestellungen:
Welche ebenen Figuren sind in der Grundschule relevant und wie lassen sie sich charakterisieren?
In der Grundschule liegt der Fokus weitestgehend auf der Betrachtung von Dreiecken, Vierecken und Kreisen. Im Folgenden werden diese beschrieben. Dabei werden wesentliche Unterrichtsinhalte bzw. Lernziele kurz skizziert. Dennoch können und sollten auch weitere Vielecke (wie Fünf- oder Sechsecke) zum Thema des Unterrichts werden.
Dreiecke
Bevor Sie mehr Informationen über Dreiecke und ihre Eigenschaften erhalten, sollen Sie sich an dieser Stelle zunächst selbst mit diesen beschäftigen.
Eigenaktivität
Kinder haben vorgegebene Dreiecke geordnet. Dadurch sind die abgebildeten Gruppierungen entstanden.
-
Welche Kriterien könnten die Kinder zur Sortierung der Dreiecke herangezogen haben?
-
Wodurch unterscheiden sich die Dreiecke? Was ist innerhalb einer Gruppierung gleich?
-
Was könnten passende Bezeichnungen für die fünf Gruppen von Dreiecken sein?

Eigenschaften
Grundschüler sollten verschiedene Arten von Dreiecken kennenlernen und die sie unterscheidenden Eigenschaften erkennen und beschreiben können. Sie sollten wissen, dass das Dreieck eine ebene Figur mit drei Ecken und drei Seiten ist. Seitenlänge und Winkelgröße können variieren, sodass verschiedenste Dreiecke möglich sind.
Es gibt Dreiecke, bei denen alle Seiten unterschiedlich lang sind; Dreiecke mit zwei gleichlangen Seiten; Dreiecke bei denen alle Seiten gleichlang sind. In der Grundschule werden noch keine Winkelgrößen gemessen oder als Zahl angegeben. Bei der Beschreibung der Winkel können die Kinder Bezug auf den rechten Winkel nehmen und beispielweise formulieren: ... ist eine spitzere Ecke als... oder auch ... ist viel mehr als der rechte Winkel. In der Grundschule genügt es, zwischen rechten und nicht rechten Winkel zu unterscheiden.
Dreiecke als Grundbaustein
Aus Dreiecken können alle weiteren Vielecke entstehen. So können zwei deckungsgleiche gleichschenklig-rechtwinklige Dreiecke zu einem Quadrat zusammengesetzt werden.

Die mathematischen Eigenschaften, die die jeweiligen Dreiecke charakterisieren, wie z.B. der rechte Winkel, können genutzt werden, um Gesetzmäßigkeiten der ebenen Figur abzuleiten und zu begründen. Legt man wie im obigen Beispiel die zwei deckungsgleichen, gleichschenklig-rechtwinkligen Dreiecke mit der Seite, die dem rechten Winkels gegenüberliegt, aneinander, erhält man ein rechtwinkliges Viereck. Es ist ein sogar ein Quadrat, da die gleichlangen Schenkel der Dreiecke die Seiten des Vierecks sind und damit alle Seiten des Vierecks gleichlang sind.
Vierecke
Eigenschaften
Grundschüler sollten wissen, dass das Viereck eine ebene Figur mit vier Ecken und vier Seiten ist. Seitenlänge und Winkelgröße können variieren, so dass verschiedenste Vierecke möglich sind. Es gibt Vierecke bei denen alle Seiten unterschiedlich lang sind; Vierecke mit zwei gleichlangen Seiten; Vierecke mit jeweils zwei gleichlangen Seiten Vierecke bei denen alle Seiten gleichlang sind.
Es kann auch variiert werden, wo die gleichlangen Seiten im Viereck liegen – ob benachbart oder gegenüberliegend, wodurch ebenfalls unterschiedliche Vierecke entstehen. Auch die Winkelgröße ist variabel. Wie beim Dreieck, ist in der Grundschule die Unterscheidung nach rechtem Winkel oder kein rechter Winkel von Interesse. Beispiele für verschiedene Vierecke, werden im folgenden Abschnitt erarbeitet und vorgestellt.
In unserer Umgebung finden wir eher spezielle Vierecke, wie Rechtecke und Quadrate. Das prägt auch das Verständnis der Kinder. Das Quadrat wird von Kindern häufig als DAS Viereck angesehen, obwohl Vierecke so vielfältig sind. Im Geometrieunterricht der Grundschule besteht damit die Herausforderung das Begriffsbild Vierecke der Kinder zu erweitern. Kinder können selbst eine Vielzahl von unterschiedlichen Vierecken erzeugen, beispielsweise durch Falten, Schneiden, Spannen oder Legen. Näheres hierzu finden Sie unten unter Zugänge für Grundschulkinder.
Vierecke in ihren vielfältigen Beziehungen
Aus einem allgemeinen Viereck (ein Viereck ohne spezielle Eigenschaften bezüglich seiner vier Ecken und vier Seiten) können durch Hinzunahme spezieller Merkmale „spezielle Vierecke“ konstruiert werden. Dies funktioniert auch andersherum: Aus einem Quadrat können durch Wegnahme bestimmter Eigenschaften andere spezielle Vierecke entstehen.
Nehmen wir ein Quadrat: Ein Quadrat hat vier gleich lange Seiten und vier rechte Winkel. Was passiert, wenn man die Seitenlänge verändert, die Winkelgröße jedoch beibehält? Damit die rechten Winkel erhalten bleiben, muss man bei der Veränderung einer Seitenlänge immer auch die gegenüberliegende Seite in gleicher Art und Weise verändern. Es entsteht somit ein Viereck mit vier rechten Winkel und jeweils zwei sich gegenüberliegenden gleichlangen Seiten. Solche Vierecke heißen Rechtecke.
Was passiert, wenn wir im Quadrat die Seitenlängen beibehalten und nur die Winkel verändern? In diesem Fall verändern sich immer zwei gegenüberliegende Winkel in gleicher Art und Weise. Es entsteht ein Viereck mit vier gleichlangen Seiten und jeweils zwei sich gegenüberliegenden gleichgroßen Winkeln. Solche Vierecke heißen Raute.
Durch Fortsetzen dieses Vorgehens entsteht das sogenannte Haus der Vierecke. Diese Darstellung bietet die Möglichkeit die innewohnende Begriffshierarchie zu nutzen, um die Beziehungen der Vierecke zueinander zu beschreiben.
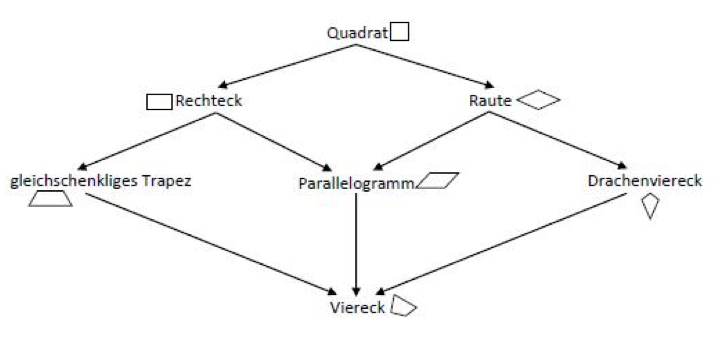 Begriffshierarchie im "Haus der Vierecke"
Begriffshierarchie im "Haus der Vierecke"
Hier finden Sie weitere Informationen zu den Eigenschaften der verschiedenen Vierecke, die mit den Kindern thematisiert werden können. Dabei stellt es eine Herausforderung dar, mit den Kindern sprachliche Mittel zu adäquaten Beschreibung zu erarbeiten. Gefundene Eigenschaften können in Form von Steckbriefen festgehalten werden. Diese können durch die Kinder selbst erstellt werden und gemeinsam zu verbindlichen Festlegungen zusammengetragen werden – dabei werden auch Begriffe festgelegt. Unter Aktivitäten in der Ebene (Sortieren) wird dies nochmals aufgegriffen.
Vielecke
Eigenschaften
Grundschüler sollten wissen, dass das Vieleck eine ebene Figur mit gleich vielen Ecken und entsprechend vielen Seiten ist. Ein n-Eck hat somit n Seiten und n Ecken (Beispiel: ein Fünfeck hat fünf Ecken und fünf Seiten). Seitenlänge und Winkelgröße können variieren, so dass verschiedenste Vielecke möglich sind.
Entdeckerpotential von Vielecken
Vierecke, wie Quadrat und Rechteck und auch die Dreiecke sind im Unterricht als Untersuchungsgegenstand sehr schnell "verbraucht". Sie zu nutzen, um andere Figuren zu erzeugen (siehe Beschreibung bei Dreiecken), erweitert den Blick zumindest auf Fünf- und Sechsecke (vgl. auch Spannen weiter unten). Eigene Aktivitäten und eine Erweiterung der Figurenformen regt die Entdeckerlust der Kinder an. Sie können Eigenschaften wiederentdecken, bekannte Gesetzmäßigkeiten übertragen und nutzen, um Neues zu finden.
Die besondere Form: Kreis
Eigenschaften
Ein Kreis ist eine gleichmäßig runde, in sich geschlossene Linie, deren Punkte alle den gleichen Abstand vom Mittelpunkt haben.
Aktivitäten, die einen Kreis entstehen lassen, helfen charakteristische Eigenschaften eines Kreises zu erkennen. So kann auf dem Schulhof um einen (Mittel)Punkt herum mit einem Seil in unveränderter Länge einen Kreis erzeugt werden. Kinder lernen so, auch das Aufbauprinzip für einen Zirkel kennen. Der Umgang mit dem Zirkel muss geübt werden.
Wie entwickeln sich Vorstellungen der Kinder zu ebenen Figuren?
Begriffe für ebene Figuren wie Dreieck, Viereck, und Kreis sind vielen Kindern bei Schuleintritt bekannt. Die Vorstellungen dazu können individuell unterschiedlich sein.
So wird z.B. das Quadrat häufig als Repräsentant für alle Vierecke angesehen. Wie oben beschrieben, handelt es sich bei dem Quadrat jedoch eher um ein sehr spezielles Viereck unter vielen verschiedenen speziellen Vierecken. Durch gezielte materialgestützte Aktivitäten wird das Begriffsbild des Kindes ergründet, erweitert, umstrukturiert und präzisiert.
So umfasst das Lernen von Begriffen den Aufbau angemessener Vorstellungen, den Erwerb von Kenntnissen und die Aneignung von Fähigkeiten. Ausgehend von Handlungen und zunächst intuitiven Vorstellungen wird über verschiedene Denkebenen, Niveaus und Stufen nach und nach ein abstrakteres Verständnis mathematischer Begriffe entwickelt (Vollrath 1984, S. 202 ff). Dabei ist zu betonen, dass das Definieren von Begriffen kein Schwerpunkt des Geometrieunterrichts der Grundschule ist. Gleichwohl gibt es viele Aktivitäten, die dazu beitragen, dass die Vorstellungen der Kinder zu ebenen Figuren ausgebaut werden. Diesen Prozess nennt man Begriffsbildung.
Bezogen auf ebene Figuren kann beispielsweise das Betrachten von Beispielen und Gegenbeispielen die Entwicklung angemessener Vorstellungen unterstützen. So kann ein exemplarisches Quadrat mit einer exemplarischen Raute verglichen werden. Während das exemplarische Quadrat als Beispiel für Quadrate im Allgemeinen dient, kann an der als Gegenbeispiel fungierenden Raute erarbeitet werden, dass neben der gleichen Länge der Seiten, eine weitere charakterisierende Eigenschaft von Quadraten ist, dass alle Winkel rechte Winkel sind. Solche Zuordnungen helfen, den Begriff von anderen Figurbegriffen abzugrenzen bzw. in das vorhandene Begriffsnetz einzuordnen.
Durch Vergleichen von ebenen Figuren können Gemeinsamkeiten und Unterschiede gefunden werden. Dazu gehören u.a. auch Lagebeziehungen von Seiten, wie gegenüberliegende, zueinander parallele bzw. zueinander senkrechte (vgl. die Ausführungen zu den Eigenschaften ebener Figuren oben). Um spezielle Eigenschaften einer ebenen Figur zu beschreiben, kann das Bedürfnis wachsen einen (neuen) Begriff zu fassen.
Grundsätzlich ist hierzu jedoch zu betonen, dass das Lernen geometrischer Begriffe ein langfristiger Prozess ist. Am Ende der Grundschulzeit sollten Kinder wissen, dass es Begriffe (Namen) für ebene Figuren und Eigenschaften sowie für Beziehungen von ebenen Figuren gibt und (zumindest grundlegende) Figuren anhand ihres Wissens unterscheiden können.
Doch wie kann ich solche Prozesse in der Grundschule nun tatsächlich anstoßen? Um dies zu verdeutlichen, werden im Folgenden einige grundlegende für die Grundschule geeignete Aktivitäten in der Ebene vorgestellt.
Welche Zugänge sind für Grundschulkinder geeignet, um Wissen über ebene Figuren zu erwerben?
Ebene Figuren wurden aus der Abstraktion der Außenwelt gewonnen. Das kann man mit Kindern nachvollziehen, indem sie gefordert werden Objekte der Umwelt zubeschreiben. Dies kann einen ersten Zugang zu ebenen Figuren ermöglichen (vgl. Einstieg). Umgekehrt wird in der Umwelt nach Objekten gesucht, in denen die ebenen Grundformen "versteckt" sind.
Die aktive Auseinandersetzung der Kinder mit geometrischen Phänomen ist im Weiteren aus zwei Perspektiven möglich. Auf der einen Seite können sich Kinder durch Handlungen (wie Sortieren, Legen, Falten etc., siehe unten) Eigenschaften und Maße von ebenen Figuren erschließen und Beziehungen in und zwischen ihnen entdecken. Auf der anderen Seite können sie aus dem Wissen über spezielle ebene Figuren auch gezielt ebene Figuren erzeugen und herstellen (ebenfalls durch Legen, Falten, Schneiden aber auch durch Zeichnen). In beiden Fällen kann der Prozess der Begriffsbildung vorangetrieben werden.
Um dies zu ermöglichen, ist es jedoch unabhängig davon, welche Perspektive verfolgt wird, wichtig immer wieder gedankliche Prozesse anzuregen, indem die Kinder aufgefordert werden, ihr Handeln und ihre Entdeckungen zu beschreiben und zu dokumentieren oder sich vor einer Materialhandlung zunächst vorzustellen, wie das fertige Bild aussieht. Ohne sprachliche Begleitung besteht die Gefahr, dass die Aktivitäten zu einer inhaltsleeren Beschäftigung (Basteln) ohne Bezug zur Geometrie und ohne das Potenzial zur Begriffsbildung werden.
Im Folgenden werden grundlegende Aktivitäten in der Ebene, die sich zum Teil für beide Perspektiven eignen, beispielhaft beschrieben und erläutert. Das Zeichnen nimmt eine gesonderte Rolle ein. Hierzu finden Sie nähere Informationen auf der Seite Zeichnen.
Sortieren
Sortieraktivitäten der Kinder haben das Ziel, geometrische Eigenschaften von ebenen Figuren in den Mittelpunkt der Betrachtungen zu stellen und geometrischen Begriffe abzuleiten bzw. einzuführen (siehe oben: Ebene Figuren und ihre Eigenschaften).
Sortieren erfordert ein genaues Beobachten und schult die Wahrnehmungsfähigkeit der Kinder. Auch ihre verbalen Fähigkeiten werden gefordert, denn entsprechend der Auswahlkriterien (Eigenschaften finden oder Eigenschaften nutzen) sind Gruppierungen zu begründen. Hierzu können auch Steckbriefe für die verschiedenen Figuren angefertigt werden.
Legen
Legen ist eine grundlegende Aktivität durch die ein Begriffsverständnis zu ebenen Figuren aufgebaut werden kann und Erfahrungen der Kinder eingebracht werden können.
Wie kann das Legen von Figuren nun konkret aussehen und was können die Kinder dabei lernen und erarbeiten? Probieren Sie das zunächst einmal selbst aus.
Eigenaktivität
Welche Figuren können Sie erhalten, wenn Sie diese zwei gleichschenkligen, aber nicht rechtwinkligen Dreiecke zusammensetzen?

-
Welche Eigenschaften haben die Figuren?
-
Wie kann man die Eigenschaften begründen?
-
Können Sie die Figuren benennen?
Wie beschrieben, können durch das Legen von ebenen Figuren neue bzw. andere ebene Figuren erzeugt werden. Dabei können die bekannten Eigenschaften der Ausgangsfiguren genutzt werden, um Eigenschaften der erzeugten Figuren abzuleiten. Im Kapitel Dreiecke wurde dies exemplarisch für die Zusammensetzung eines Quadrats aus zwei deckungsgleichen gleichschenklig-rechtwinkligen Dreiecken erläutert. Auch in der Eigenaktivität wurde dies deutlich. Kennen die Kinder die Eigenschaften der vorgegebenen Dreiecke können sie sich auch die Eigenschaften der Vierecke erschließen. Das Vorgehen lässt sich grundsätzlich auch auf andere ebene Figuren übertragen.
Auch beim Zusammensetzen gleichseitiger Dreiecke oder rechtwinkliger Dreiecke ergeben sich spezielle Vierecke. Diese Aufgabenstellung ist darüber hinaus vielfältig variierbar. So können durch Hinzunahme weiterer (kongruenter) Dreiecke auch Fünf- und Sechsecke entdeckt werden.
Ähnliche Aktivitäten und (umgekehrte) Fragestellungen in diesem Zusammenhang können auch sein:
-
Kann ich in einem gegebenen Viereck Dreiecke entdecken? Welche Eigenschaften haben diese? Was weiß ich über meine Ausgangsfigur? Was bedeutet das für die Teildreiecke?
-
Wie kann ich durch falten (oder schneiden) in Teildreiecke die besonderen Eigenschaften eines gegebenen Vierecks, z. B. eines Drachenvierecks, prüfen?
Solche Aktivitäten und Überlegungen fördern die Begriffsbildung, da sie dazu beitragen, dass sich die Vorstellungen der Kinder zu ebenen Figuren ausdifferenzieren und Fachbegriffe inhaltlich angereichert werden (vgl. Wie entwickeln sich Vorstellungen der Kinder zu ebenen Figuren?).
Nicht zuletzt wird bei solchen Aktivitäten auch die Nutzung der Fachsprache gefördert. Die Kinder werden schnell merken, dass Begriffe (wie Ecke, Seite, länger, kürzer, gleichlang, usw.) wichtig sind, um sich anderen verständlich zu machen und Auffälligkeiten und Eigenschaften eindeutig zu beschreiben oder zu begründen.
Für das Legen können unterschiedliche Flächenformen (heterogenes Material), so beispielsweise die verschiedenen Formen aus dem Tangram, ausgewählt werden. Das Legen mit homogenem Material, wie gleichlangen Hölzchen oder gleichgroßen Quadraten bietet vielfältige Möglichkeiten der Aufgabenkonstruktion und Variation. Beim Legen unterscheidet man weiterhin: Legen nach Vorgaben, Nachlegen, Umlegenund Auslegen von ebenen Figuren. Konkrete Aktivitäten hierzu werden im Unterrichtsteil am Beispiel des Tangrams beschrieben.
Zum Legen gehört auch das Fortsetzen z. B. Ornamente aus homogenem oder auch heterogenem Material fortsetzen (vgl. auch Symmetrie).
Weitere Anregungen finden Sie auf den Seiten unseres Partner-projekts PIK AS:
PIKAS: Unterrichtsmodul – Gute Aufgaben .
Spannen
Das Spannen von ebenen Figuren liefert im Ergebnis eine Darstellung. Wesentliche Eigenschaften ebener Figuren werden sichtbar. Im Fall des Rechtecks sind das: zwei Paare gleichlanger und paralleler gegenüberliegender Seiten sowie rechte Winkel.
Freies Spannen ist geeignet, um ein Material, wie beispielsweise das Geobrett einzuführen und um den Kindern die Möglichkeit zu geben, sich mit der Handhabung vertraut zu machen. Beim Spannen unterscheidet man weiterhin: Spannen von ebenen Figuren nach Vorgaben und nach Angabe von Arbeitsschritten.
Darüber hinaus können bei dargestellt Figuren auch Seitenlängen und Lagen verändert werden und die Auswirkungen in Bezug auf die Formeigenschaften beschrieben werden. Weitergehende Entdeckungen wie Symmetrien, Drehungen bzw. Flächeninhaltsvergleiche können angeregt werden. Hierzu finden Sie in Selter & Zannetin 2018(S. 110-114) weitere Informationen und Unterrichtsideen.
Falten
Falten bietet den Kindern oft einen ersten Zugang zum Verständnis geometrischer Inhalte (vgl. Symmetrie). Faltübungen sind geeignet, um Kinder wichtige Merkmale der Grundfiguren entdecken zu lassen. Neben dem Umriss einer Figur wird auch die Fläche sichtbar. Winkel können verglichen werden, ohne dass Winkelmaße bekannt sind.
Durch einfache Faltübungen können einige grundlegende Begriffe anschaulich geklärt werden (vgl. Franke & Reinhold 2016, S. 231)
-
Ecke, Seite, Diagonale
-
Mittellinie, Mittelpunkt
-
benachbarte Seite/gegenüberliegende Seite
-
rechts/links, oben/unten, innen/außen
Diese Begriffe gehören zum zu erlernenden Fachvokabular im Bereich der Geometrie. Sie sind zudem von Bedeutung, um Faltanleitungen zu verstehen bzw. eigene Handlungen beschreiben zu können.
Weitere Anregungen zum Falten finden Sie auch auf den Seiten unseres Partnerprojekts PIK AS unter PIKAS: Unterrichtsmodul: Raum und Form – Symmetrie – Faltschnitte.
An dieser Stelle soll nochmals betont werden, dass bei allen Aktivitäten selbstverständlich eine sprachliche Begleitung erforderlich ist. Kinder sollten gefordert sein, ihr Vorgehen zu beschreiben, zu begründen und zu dokumentieren. Ein zielgerichteter Austausch dazu unterstützt den Erkenntnisgewinn der Kinder, lässt sie Zusammenhänge begreifen und zielführende Aktivitäten erkennen. Konkretisiert wird dies im Folgenden in den Ausführungen im Unterricht zur Aktivität „Legen“.