Vorstellungen über grundlegende geometrische Begriffe und Fähigkeiten im Umgang mit Körpern entwickeln
Kinder entdecken ihre Umwelt in dem sie Körper wahrnehmen, sie im wahrsten Sinne des Wortes begreifen und Körper nutzen, um ihre Umwelt nachzubilden. So erschließen sich Kinder bereits vor Schuleintritt Eigenschaften von Körpern und lernen Bezeichnungen kennen, die sie für die Gestaltung und die Beschreibung ihrer Handlungen und ihrer Umwelt nutzen. In welchem Umfang das geschieht, hängt von den konkreten Erfahrungsmöglichkeiten und Aktivitäten des einzelnen Kindes ab.
Im Geometrieunterricht der Grundschule ist der Umgang mit verschieden geometrischen Körpern zu ermöglichen, um vielfältige Entdeckungen im Raum zuzulassen. So können grundlegende Kenntnisse über Körper herausgestellt werden und sich Fähigkeiten und Fertigkeiten im Operieren mit Körpern entwickeln. Diese ermöglichen es, Beziehungen zwischen den Körpern zu erkennen und zu nutzen sowie eine adäquate Sprachkultur zu etablieren. Damit wird räumliches Vorstellungsvermögen geschult und die geometrische Begriffsbildung unterstützt.
Auf dieser Seite erhalten Sie Hintergrundinformationen zu folgenden zentralen Aspekten:
Experimentelle und zielgerichtete Aktivitäten, flankiert von sprachlicher Begleitung und Reflexion des Handelns, unterstützen das Erkunden von geometrischen Besonderheiten der einzelnen Körper. Mit Fühlen, Anfassen, Begreifen von räumlichen Gegenständen erschließen sich bereits die Jüngsten vor Schuleintritt ihre Umgebung.
Das Ertasten von Körpern und das Verbalisieren der Vorstellungen trägt dazu bei charakteristischen Eigenschaften des Gegenstandes herauszustellen. Diese sind Grundlage, um andere Repräsentanten zu erkennen und zuzuordnen. Dieses Herangehen fördert einerseits Raumvorstellungsvermögen und andererseits ist es grundlegend für die Begriffsbildung.
Geometrische Begriffe haben sich durch Abstraktion aus der Umwelt entwickelt. Für den Grundschulunterricht bedeutet das, dass Grundbegriffe, die der Erfahrungswelt der Kinder entsprechen und anschaulich klar sind, als Bezeichnungen vereinbart werden. Dabei greift man auch die Bezeichnungen auf, die sich umgangsprachlich etabliert habe und von den Kindern bei Schuleintritt verwendet werden.
Das Lernen von Begriffen umfasst den Aufbau angemessener Vorstellungen, den Erwerb von Kenntnissen und die Aneignung von Fähigkeiten. Ausgehend von Handlungen und zunächst intuitiven Vorstellungen, wird über verschiedene Denkebenen, Niveaus und Stufen ein abstrakteres Verständnis der mathematischer Begriffe entwickelt (Vollrath 1984, S. 202 ff).
In den Bildungsstandards gibt es keine Vorgaben bzw. Einschränkungen auf bestimmte Körper, die Gegenstand des Geometrieunterrichts der Grundschule sein sollen. Ein Blick in die Lehrpläne zeigt, dass der Fokus in den Jahrgangsstufen 1 und 2 weitestgehend auf der Betrachtung von Würfel, Quader und Kugel liegt und in den folgenden Jahrgangsstufen 3 und 4 auf Zylinder, Pyramide und auch Kegel erweitert wird.
Im Folgenden werden die für die Grundschule wesentlichen Eigenschaften der genannten Körper beschrieben.
Würfel
Eigenschaften
Ein Würfel ist ein Körper mit acht Ecken, sechs Flächen und zwölf Kanten. Alle Flächen bestehen aus gleich großen (deckungsgleichen) Quadraten. In den Kanten stoßen zwei Flächen im rechten Winkel aufeinander. Alle Würfel sind zueinander ähnlich und unterschieden sich nur in ihrer Größe.
Durch den Umgang mit Spielwürfeln haben Kinder bereits zu Schulbeginn Vorstellungen vom Würfel. Der Begriff wird jedoch häufig eher mit dem Gegenstand selbst als denn mit seinen Eigenschaften in Verbindung gebracht. Um diese herauszustellen sind vielfältige Aktivitäten mit Würfeln notwendig, da Spielewürfel z.B. abgerundete Ecken haben und auch traditionelle Bezeichnungen wie „Würfelzucker“ für heute eher quaderförmige Zuckerstücke zudem auf einen fälschlichen Gebrauch der Bezeichnung „Würfel“ in der Umgangssprache verweisen.

Quader
Eigenschaften
Ein Quader ist ein Körper mit acht Ecken, sechs Flächen und zwölf Kanten. Alle Flächen sind rechteckig. In den Kanten stoßen zwei Flächen im rechten Winkel aufeinander. Gegenüberliegende Flächensind gleich groß (deckungsgleich) (Franke & Reinhold 2016, S. 197)
Wie bei den ebenen Figuren (Haus der Vierecke) kann man auch hier die Beziehungen zwischen Quader und Würfel, als speziellem Quader betrachten. Ein tieferes Verständnis wird auch schon bei Grundschulkindern erreicht, wenn man Untersuchungen auf die Beziehungen zwischen Würfel und Quader erweitert.

Kugel
Eigenschaften
Eine Kugel hat keine Ecken und eine gleichmäßig gekrümmte Oberfläche.
Alle Kugeln sind zueinander ähnlich und unterschieden sich nur in ihrer Größe.
Diese Besonderheiten unterscheidet die Kugel nicht nur von den anderen Körpern, sondern insbesondere auch vom (ebenen) Kreis, der oft für die Darstellung bzw. Abbildung einer Kugel genutzt wird. Die Kugel ist die Menge aller Punkte des Raumes, die von einem gegebenen Punkt M (dem Mittelpunkt) einen Abstand haben, der kleiner oder gleich einem festen Wert r (dem Radius) ist. Mit dem Begriff Kugel wird, je nach Kontext, die Oberfläche betrachtet oder der Vollkörper.

Zylinder
Eigenschaften
Ein (gerader) Zylinder hat zwei gekrümmte Kanten und keine Ecken. Grund- und Deckfläche sind deckungsgleiche Kreise, die parallel zueinander liegen. Die Mantelfläche ist gleichmäßig gekrümmt, in sich geschlossen und ergibt beim Abrollen ein Rechteck.
Für die Entwicklung tragfähiger Vorstellungen zum Zylinder sollten unterschiedlichste Objekte aus der Umgebung gewählt werden. Insbesondere sollten die Höhen und das Größenverhältnis zwischen Durchmesser der Deck-/Grundfläche und der Höhe des Zylinders variiert werden. Es sollte zudem auf den Begriff Hohlzylinder eingegangen werden, dessen Repräsentanten im Umfeld der Kinder in vielfältiger Form zu finden sind.

Pyramide
Eigenschaften
Eine (gerade) Pyramide hat als Grundfläche ein Vieleck (Dreieck, Viereck, Fünfeck, ...). Danach richtet sich die Anzahl der Seitenflächen, die gleichschenklige Dreiecke sind. Diese enden in einer gemeinsamen Spitze. Die Anzahl der Kanten und Ecken wird durch die Grundfläche bestimmt.
Ägyptische Pyramiden haben in der Regel das Begriffsbild der Grundschulkinder geprägt. Im Unterricht geht es also darum, dies zu erweitern. Das kann gelingen, wenn die Grundfläche in vielfältiger Weise variiert wird: von einer quadratischen zu einer dreieckigen oder rechteckigen bis hin zu einer fünfeckigen Grundfläche. Der Vergleich dieser Körper lässt die wesentlichen Eigenschaften von Pyramiden erkennen und die speziellen Merkmale der einzelnen.

Kegel
Eigenschaften
Der (Kreis)Kegel hat eine kreisförmige Grundfläche. Darüber befindet sich eine gleichmäßig gekrümmte Fläche, die in einer Spitze endet.
Ob Eistüte, Vulkankegel oder Sandkegel, der beim Spielen entstehen kann, Kinder kennen eine Reihe unterschiedlicher Repräsentanten eines Kreiskegels. Ein Vergleich mit anderen Körpern schärft den Blick der Kinder für charakteristische Eigenschaften der einzelnen Repräsentanten und unterstützt die Entwicklung von Begriffsinhalt und –umfang.

Körper können auf verschiedene Weise – in Form von Modellen – repräsentiert und dargestellt werden.
So unterscheiden wir zum einen zwischen:
Körper als massive Modelle - Als Holzbausteine kennen und nutzen Kindern massive Modellegeometrischer Körper bzw. Bauwerke bereits vor Schuleintritt. Massive Modelle können darüber hinaus gemeinsam mit den Kindern hergestellt werden. Knete ist dazu gut geeignet, da sie sich gut (um)formen und auch teilen lässt. Kinder sind beim Herstellen gefordert sich mit den charakteristischen Eigenschaften eines Körpers auseinanderzusetzen. Zerschneidet man derartige Modelle, das auch auf unterschiedliche Art und Weise, entstehen neu Körper, die weiter untersucht werden können.
 Bildunterschrift
Bildunterschrift
Körper als Kantenmodelle - Kantenmodellebieten vielfältige Möglichkeiten, Erkenntnisse über Anzahl von Ecken und Kanten zu veranschaulichen. Es können Beziehungen (Lage, Längenvergleich) zwischen den Kanten betrachtet und Aussagen untersucht werden.
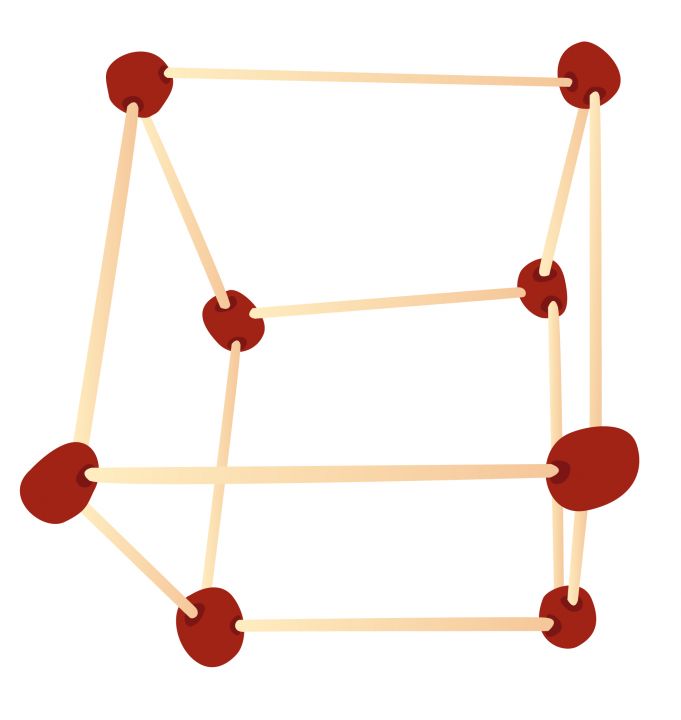
Körper als Körpernetze (Flächenmodelle) - Körpernetze sind zweidimensionale Figuren, in denen ebene Figuren so verbunden sind, dass daraus ein Körper gefaltet werden kann (Franke & Reinhold, 2016). Durch wiederholtes Kippen eines Körpers, Umfahren der jeweiligen Liegefläche bzw. Abrollen gekrümmter Flächen können derartige Netze entstehen.
Umgekehrt kann untersucht werden, ob aus einer Anordnung von ebenen Figuren, beispielsweise Anordnung von sechs Quadraten, ein Körper – in diesem beispiel ein Würfel - zusammengefaltet werden kann. In diesem Zusammenhang ist die Frage interessant, welche Anordnungen von sechs Quadraten Würfelnetze darstellen.
Zum anderen sind zur Sicherung von Arbeitsergebnissen und auch als Vorlage für Handlungsanweisungen grafische und verbale Darstellungen von Körpern unumgänglich. In diesem Kontext werden unterschiedliche Ansichten, perspektivische Darstellungen, Baupläne und verbale Beschreibungen zentral.
Fordert man Kinder auf, eigene Bauwerke darzustellen, so zeichnen sie einerseits Ansichten des Körpers aus verschiedenen Perspektiven – von vorn, von den Seiten, von oben, gelegentlich auch von unten. Damit nutzen sie schon typische Zusammenstellung von Ansichten (Vorderansicht, Seitenansicht, Draufsicht). Darüber hinaus gibt es Baupläne. Dabei wird im Grundriss des Körpers die jeweilige Anzahl der übereinander angeordneten Würfel angegeben.
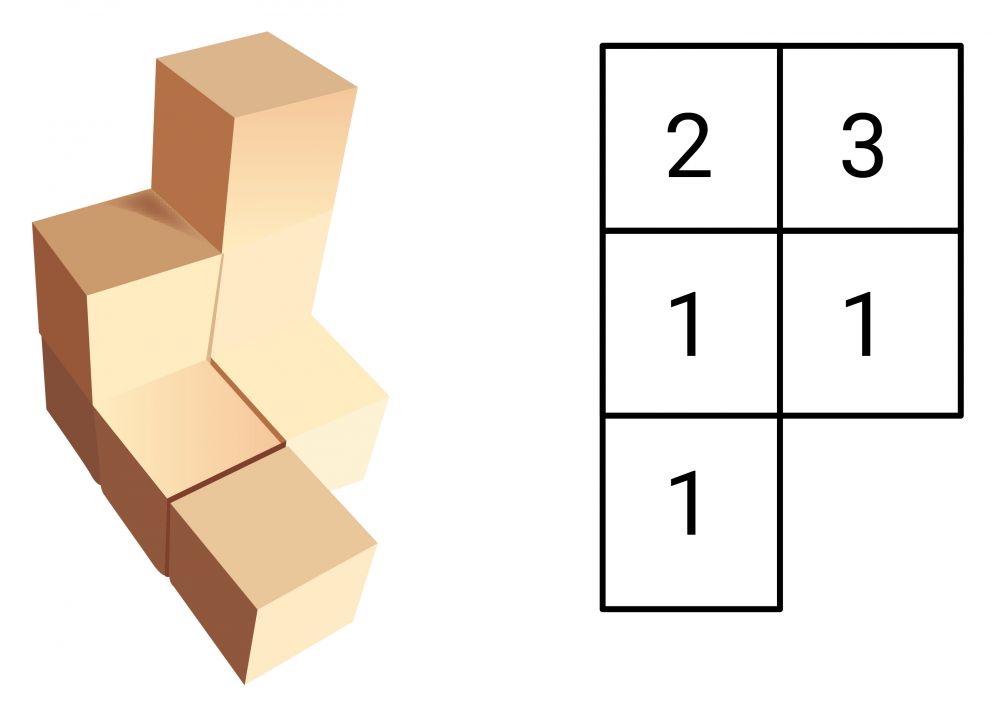
Übergeordnet sind verbale Darstellungen geeignet, um einen Körper zu beschreiben. Umgekehrt kann man nach einer Beschreibung einen Köper bauen. Dies gilt nicht nur für verbale Darstellungen. Jede der aufgeführten Darstellungen kann Ausgangspunkt sein, um einen Körper herzustellen bzw. Darstellungen in einander zu überführen. Zu diesen grundlegenden Aktivitäten mehr im folgenden Abschnitt.
Um Körper ganzheitlich zu erfahren und die charakteristischen Eigenschaften zu erarbeiten und miteinander in Beziehung zu setzen, sollten im Unterricht verschiedene Modelle und Darstellungen zum Gegenstand der gemeinsamen Auseinandersetzung werden. Wichtig ist, dass dabei unterschiedliche Repräsentationsebenen angesprochen und Kinder lernen, zum einen zwischen diesen wechseln zu können und sie dabei auch miteinander vernetzen (vgl. Franke & Reinhold 2016, S. 24).
So sehen wir die folgenden Aktivitäten als grundlegend an, in denen auch das Herausarbeiten von Gemeinsamkeiten und Unterschieden zwischen Körpern zentral wird und somit zum Aufbau eines differenziertes Begriffsverständnis beitragen:
Sortieren und Identifizieren - Beim Sortieren rücken die geometrischen Eigenschaften der einzelnen Körper in den Mittelpunkt der Betrachtungen. Indem diese erkannt, voneinander unterschieden und die geometrischen „Kriterien“ verbalisiert werden, trägt diese Auseinandersetzung zur Begriffsbildung bei. Solche geometrischen Kriterien könnten sein:
-
Anzahl der Ecken
-
Anzahl der Flächen
-
Anzahl der Kanten
-
Form der Fläche und Lage dieser Flächen
-
Größe der Objekte (Länge der Kanten, Länge, Breite, Höhe)
-
Größe der Winkel innerhalb der Objekte
Beim Sortieren und Identifizieren können die verschiedenen Darstellungen von Körpern (massive Modelle, Kantenmodelle, Flächenmodelle) ebenso wie grafische Darstellungen von Körpern als Ausgangspunkt genutzt werden. Von enormer Wichtigkeit ist es, über die Kriterien, die zum Sortieren genutzt und die für das Identifizieren von Körpern benötigt werden zu sprechen.
Insofern findet beim Sortieren und Identifizieren immer eine Darstellungsvernetzung zwischen dem jeweiligen Modell/der jeweiligen grafischen Darstellung und der verbalen Darstellung statt. Ebenso denkbar ist es auch Körper in verschiedenen Darstellungen zu betrachten. Dabei kann untersucht werden wie die Körper in verschiedenen Darstellungen aussehen und was das charakteristische des Körpers ist.
Erstellen und Interpretieren - Konkrete Handlungen (enaktive Repräsentationen), wie z. B. das Bauen eines Würfelvierlings aus Steckwürfeln, ermöglichen jedem Kind einen Zugang zu geometrischen Sachverhalten. Diese Handlungen schulen die Wahrnehmung wesentlicher Eigenschaften und lassen „innere“ Bilder (ikonische Repräsentation) entstehen. Verbale Beschreibungen gehören zur symbolischen Repräsentationsebene. Kinder greifen dabei auf ihre Vorstellungen zurück und nutzen ihre sprachlichen Fähigkeiten.
Um die Fähigkeiten auf den unterschiedlichen Repräsentationsebenen zu entwickeln, sollten Kinder gefordert werden, nicht nur unmittelbar einen Körper zu bauen, sondern auch weitere Darstellungen eines Körpers herzustellen bzw. auch verschiedene Darstellungen ineinander zu überführen bzw. aus der verbalen Beschreibung eines Körpers ein Kantenmodell zu erstellen oder einen Körper der im Kantenmodell vorliegt zu zeichnen.
Dazu wurden inzwischen auch computerunterstützen Lernumgebungen entwickelt. Als Beispiel sei hier die Klötzchen-App genannt. Es können u. a. verschiedene Darstellungen (realistische Abbildung, Bauplan, Zweitafelbild, isometrische Darstellung, Schrägbild) nebeneinander betrachtet werden.
Es ist also wichtig, die Darstellungen zusammenzuführen und zu vernetzen.
Diese Darstellungswechsel unterstützen die Begriffsbildung und erweitern vor allem die Artikulationsmöglichkeiten der Kinder. So kann der „Rückgriff“ auf ein Körpermodell einem Kind Sicherheit geben, wenn es diesen Körper beschreibt. Dadurch werden die sprachlichen Fähigkeiten des Kindes weiterentwickelt.