Symmetrie in der Grundschule
Im Folgenden sollen folgende Fragen erörtert werden:
Zunächst sollen Sie sich jedoch mit ihrem eigenen Symmetriebegriff auseinandersetzen.
Eigenaktivität
Betrachten Sie die folgenden drei Abbildungen. Welche Symmetrien können Sie feststellen?
Worauf achten Sie bei Ihren Überlegungen?
 Abb. 1
Abb. 1
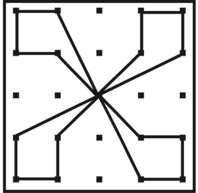 Abb. 2 (vgl. Götze 2016)
Abb. 2 (vgl. Götze 2016)
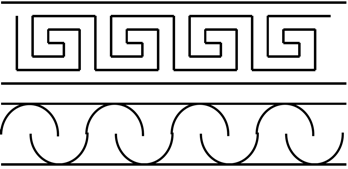 Abb. 3 (vgl. Pikas, Sachinformationen Haus 2.3)
Abb. 3 (vgl. Pikas, Sachinformationen Haus 2.3)
Was ist Symmetrie?
Der Begriff Symmetrie stammt vom griechischen Wort „symmetria“ und bedeutet Ebenmaß.
„Symmetrie ist eine Eigenschaft von Figuren, bei der eine Figur oder ein räumliches Objekt durch eine Kongruenzabbildung auf sich selbst abgebildet werden kann.
Diese Kongruenzabbildung ist von der Identität verschieden und wird auch als Deckabbildung bezeichnet. Der Begriff Symmetrie wird dabei sowohl für die Eigenschaften der abgebildeten Figuren als auch für die Abbildung verwendet, die zu dieser Eigenschaft führt.“ (Franke und Reinhold 2016, S. 262).
Wie Sie bereits in der Eigenaktivität erfahren konnten, geschieht diese Deckabbildung durch Drehen, Verschieben, Spiegeln oder Kombinationen dieser Abbildungen. Dabei bleiben die Längen und Winkelmaße gleich, Formen bleiben also erhalten (vgl. Merschmeyer- Brüwer 2013, S. 6).
Kinder haben aus ihrer Lebenswelt intuitive Vorerfahrungen zur Symmetrie, beispielsweise durch die Wahrnehmung symmetrischer „Gleichheiten“ an sich selbst oder an Tieren (z. B. Schmetterlinge, Käfer) oder bezogen auf die Funktionalität von symmetrischen Gegenständen: Eine schiefe Papierschwalbe fliegt schlecht bzw. nicht geradeaus, ein Stuhl mit ungleichen Beinen wackelt.
Der Unterricht sollte dieses intuitive Vorwissen ebenso aufgreifen wie vorschulische Erfahrungen beim Malen (z.B. Klecksbilder) oder beim Falten (vgl. Franke und Reinhold 2016, S. 259).
Welchen Symmetriebegriff brauchen Grundschulkinder?
Zentral ist ein adäquates Abbildungsverständnis, das in der Grundschule mit Hilfe der Achsenspiegelung propädeutisch erarbeitet wird, da die Achsenspiegelung besonders anschaulich ist (vgl. Merschmeyer-Brüwer). Außerdem lassen sich alle anderen Kongruenzabbildungen in der Ebene aus Achsenspiegelungen aufbauen (Franke und Reinhold 2016, S. 262).
„Trotz dieser grundlegenden Bedeutung der Achsensymmetrie ist es notwendig, dass bereits Grundschulkinder lernen, symmetrisch nicht mit achsensymmetrisch gleichzusetzen. Drehsymmetrie und Verschiebungssymmetrie sollten ebenfalls betrachtet werden“ (Ruwisch 2016, S. 2).
In den Bildungsstandards lassen sich die auf den Symmetriebegriff bezogenen Kompetenzen in den Inhaltsbereichen „Raum und Form“ und „Muster und Strukturen“ verorten. Auch die prozessbezogenen Kompetenzen werden auf vielfältige Weise angesprochen. In der folgenden Abbildung werden die angesprochenen Kompetenzen übersichtlich dargestellt (in Anlehnung an Merschmeyer- Brüwer 2013):
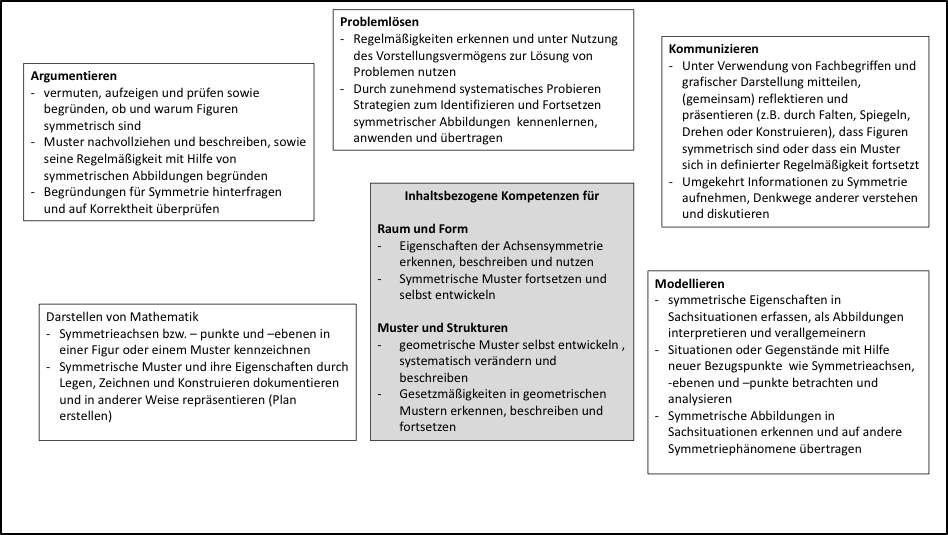 Abb. 4 Inhalts- und prozessbezogene Kompetenzen Thema "Symmetrie" (vgl. KMK 2005, leicht verändert nach Merschmeyer-Brüwer 2013, S. 7)
Abb. 4 Inhalts- und prozessbezogene Kompetenzen Thema "Symmetrie" (vgl. KMK 2005, leicht verändert nach Merschmeyer-Brüwer 2013, S. 7)
Dabei wird deutlich, dass in der Grundschule die Achsenspiegelung als zentrale Abbildung in den Mittelpunkt gerückt wird, die anderen Abbildungen durch den Blick auf geometrische Muster aber einbezogen werden müssen. Dadurch kann ein einseitiger Symmetriebegriff verhindert werden.
Wie kann der Symmetriebegriff entwickelt werden?
Bei der Entwicklung des Symmetriebegriffs sind zwei Prozesse wesentlich: Das Herstellen symmetrischer Figuren und das Analysieren gegebener symmetrischer Figuren. Wichtig ist, dass die Begriffsentwicklung Zeit und vielfältige Erfahrungen benötigt, d.h. die Thematik sollte nicht isoliert in nur einer Einheit behandelt werden, sondern durch verschiedene Zugänge im Sinne des Spiralprinzips wiederholt aufgegriffen werden (vgl. Ruwisch 2013).
Symmetrie als Eigenschaft einer Figur (wie z.B. die drei Symmetrieachsen innerhalb des Dreiecks oben, Abb. 1) ist dabei leichter zugänglich als das Erkennen einer Relation zwischen Figuren, also zueinander symmetrischer Figuren (die Symmetrie zwischen den beiden Dreiecken, Abb.1).
Bei der achsensymmetrischen Ergänzung fällt das Ergänzen nur auf einer Seite der Achse leichter als das Ergänzen auf beiden Seiten der Achse (vgl. Abb. 5).
Auch ältere Schülerinnen und Schüler haben größere Schwierigkeiten, Symmetrien zu erkennen, wenn die Symmetrieachse horizontal oder schräg zur Bildkante verläuft (vgl. die verschiedenen Symmetrieachsen innerhalb des Dreiecks, Abb. 1).
Folgende Entwicklungsschritte zum Begriffsverständnis der Achsensymmetrie (nach Schmid und Ruwisch 2016, S. 5) verdeutlichen, welche zentralen Erkenntnisse im Laufe der Zeit erarbeitet werden müssen, ohne dass damit eine Stufenfolge impliziert werden soll.
Ausgangspunkt
Figuren werden als Ganzes betrachtet und „per Augenschein“ als symmetrisch oder unsymmetrisch wahrgenommen (ohne, dass die Begriffe bereits bekannt sein müssen.
Erkenntnis
Achsensymmetrische Figuren bestehen aus zwei Hälften, die sich bzgl. einer Geraden (der Symmetrieachse) genau gegenüberliegen.
Eigenschaftsbegriff
Achsensymmetrische Figuren sind Figuren, die aus spiegelsymmetrisch angeordneten Teilen bestehen.
Ausgangspunkt
Herstellungsverfahren wie Faltschnitte, Falten und Durchpausen, Klecksbilder
Erkenntnis
Markante Punkte beider Hälften liegen zusammengefaltet genau aufeinander und sind somit gleich weit von der Faltkante (Symmetrieachse) entfernt.
Eigenschaftsbegriff
Achsensymmetrische Figuren sind Figuren, bei denen entsprechende Punkte beider Hälften (Punkt und Bildpunkt) den gleichen Abstand zur Symmetrieachse haben.
Ausgangspunkt
Herstellungsverfahren wie ergänzendes Zeichnen auf Karopapier, Spannen von Figuren auf dem Geobrett, Falten und Durchstechen
Perspektivisch: Nutzen eines Geodreiecks
Erkenntnis
Damit die Lage der Punkte beider Hälften zueinander spiegelbildlich zueinander passt, müssen diese auf einer Senkrechten zur Symmetrieachse liegen.
Eigenschaftsbegriff
Achsensymmetrische Figuren sind Figuren, bei denen entsprechende Punkte beider Hälften (Punkt und Bildpunkt) im gleichen Abstand auf einer Senkrechten zur Symmetrieachse liegen.
Es gibt unterschiedliche Zugänge zur Symmetrie, die sich in der Grundschule umsetzen lassen. Um die oben angesprochenen inhalts- und prozessbezogenen Kompetenzen zu erreichen, reicht es dabei nicht, auf der bloßen Handlungsebene zu verbleiben. Es ist notwendig, das Vorstellungsvermögen der Kinder bewusst herauszufordern, Kommunikation anzuregen und vielfältige Reflexionen anzuregen.
-
Legen (achsen-)symmetrischer Figuren
In Anknüpfung an das Legen ebener Figuren werden Figuren spiegelbildlich ergänzt. Ein randloser Handspiegel kann dabei zur Überprüfung eingesetzt werden. Die Linie, auf der der Spiegel steht, wird als Spiegelachse benannt und die Kinder lernen, „dass man solche Figuren, die eine Spiegelachse haben, symmetrisch nennt“ (Franke und Reinhold 2016, S. 270).
Wichtig ist dabei, wie bei allen geometrischen Inhalten, durch das konkrete Handeln – also Legen, Spiegeln, Zeichnen, Überprüfen – eigene Erfahrungen zu machen und diese Handlungen dann aber sprachlich zu begleiten. Die Erfahrungen müssen auch reflektiert und systematisiert werden. Auch hier sollten immer wieder gedankliche Prozesse angeregt werden, indem die Kinder aufgefordert werden, sich zunächst vorzustellen, wie das fertige Bild aussieht.
Auch Figuren mit anderen Symmetrien lassen sich legen (siehe z. B. Abbildung 8).
Auch über das Falten kann ein erster Zugang umgesetzt werden. Rechtecke, Quadrate oder auch gleichschenklige Dreiecke können so gefaltet werden, dass die Seiten genau aufeinander fallen. Dabei wird die Deckungsgleichheit der beiden Teile sichtbar, es ist erkennbar, welche Seiten gleichlang sind. Auch Formen, bei denen keine Achsensymmetrie vorliegt, können über das Falten erkennbar werden (z.B. ein Parallelogramm).
-
Falten und Schneiden (siehe auch Unterricht)
Einfache Faltschnitte, wie z.B. ein Herz oder ein Tannenbaum können aus einmal gefalteten Papieren durch Ausschneiden der halben Form hergestellt werden. Die Faltlinie als Symmetrieachse wird gekennzeichnet und benannt (vgl. z.B. pikas.dzlm.de/315).
Durch mehrfaches Falten und Schneiden entstehen Figuren, die mehrere Symmetrieachsen haben (und evtl. auch Dreh- oder Schubsymmetrien aufweisen) sind, wie Figurenketten, Deckchen, Sterne oder Kristalle. Für die Schulung der Raumvorstellung ist dann vor allem die Reflexion über die entstehenden Figuren ertragreich (aus Franke und Reinhold 2016, S. 272 f.):
-
Welche Figur entsteht nach dem erneuten Auffalten?
-
Wo befindet sich der ausgeschnittene Schnipsel nach dem Auffalten, wenn ich hier schneide?
-
Wie muss ich an dieser Kante schneiden, um ein Quadrat, ein Dreieck oder einen Kreis zu erhalten?
-
Wer findet Paare aus fertigen Deckchen oder Sternen und den passenden Ausschnitten?
-
...
Auch hier geht es wieder darum, gedankliche Prozesse anzuregen.
-
Aktivitäten mit dem Spiegel
Erfahrungen mit Spiegelbildern haben Kinder aus ihrem Alltag. An diese Erfahrungen kann und sollte im Unterricht angeknüpft werden, wenn mit einem Spiegel experimentiert wird. „So untersuchen die Kinder, was passiert, wenn
-
der Spiegel auf einer Figur an verschiedenen Stellen aufgesetzt wird,
-
der Spiegel nicht nur senkrecht, sondern in verschiedenen Winkeln zur Figur aufgesetzt wird,
-
der Spiegel zur Figur hin bzw. von der Figur wegbewegt wird“ (Franke 2016, S. 274).
Aufgaben dieser Art finden sich in den Schulbüchern, aber auch in anderen Materialien, z.B. in Spiegel (1996).
Durch zwei beweglich aneinander befestigte Spiegel entsteht ein „Spiegelbuch“, das Mehrfachspiegelungen ermöglicht.
Der MIRA- Spiegel, ein halbdurchlässiger Plexiglasspiegel, ermöglicht es, neben dem Spiegelbild auch das hinter dem Spiegel liegende Bild zu sehen. Das Spiel „Mirakel“ greift diese Möglichkeit auf (Spiegel und Götze 2008).
Weitere Spiele, wie „Reflexion“ oder das „Spiegel-Tangram“ (Spiegel, Knapstein & Thöne 2005; Thöne 2011) verbinden das Legen achsensymmetrischer Figuren mit dem Spiegeln, indem geometrische Formen so vor einen Spiegel gelegt werden, dass eine bestimmte Zielfigur entsteht.
-
Klecksbilder
Klecksbilder, wie Kinder sie häufig schon im Kindergarten erstellen,
bieten ebenfalls einen Zugang zur Achsensymmetrie.
Die dabei entstehenden Bilder lassen sich vor allem gut auf
Störungen in der Symmetrie untersuchen, da die Figuren in der Regel nicht 100%tig abgebildet werden.
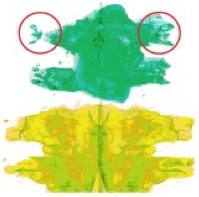 Abb. 5
Abb. 5
Zeichnen mit Hilfe von Karopapier
Auf Karopapier lassen sich achsensymmetrische Figuren, ähnlich wie beim Legen, gut zeichnerisch ergänzen. „Beim Zeichnen in Kästchen erkennen die Kinder, dass Bild und Original gleich weit von der Spiegelachse entfernt, entsprechende Strecken gleich lang und Winkel gleich groß sind“ (Franke und Reinhold 2016, S. 279).
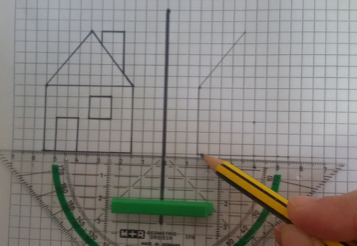 Abb. 6
Abb. 6
Symmetrie im Raum
Alle bisher beschriebenen Zugänge fokussieren auf die Achsensymmetrie in der Ebene. In der Lebenswelt kommen Symmetrien aber auch als Ebenensymmetrie im Raum vor. Der Spiegel stellt eigentlich eine solche Spiegelebene dar, keine Achse. Dies sollte bewusst thematisiert werden. Eine Möglichkeit stellen Rasch und Schmitt Ferreira (2013) vor: Kinder bauen im Klassenraum ein „Land der Spiegelsymmetrie“ auf (vgl. Abb. 7).
 Abb. 7
Abb. 7
-
Muster, Bandornamente, Parkette
In Mustern, Bandornamenten und Parketten finden sich ebenfalls vielfältige Symmetrien wieder, die die Beschäftigung mit weiterführenden Fragstellungen anregen. Hier finden sich dreh- und schubsymmetrische Elemente, die das Symmetrieverständnis über die Achsensymmetrie hinaus erweitern können (Abb. 8)
 Abb. 8 Parkette legen mit "Pattern Blocks" (Foto: Daniela Götze)
Abb. 8 Parkette legen mit "Pattern Blocks" (Foto: Daniela Götze)