Was gehört zu einem umfassenden Operationsverständnis?
Ein zentraler Inhalt im Mathematikunterricht der Grundschule ist, wie auch in den Bildungsstandards (vgl. KMK 2004, S. 9) gefordert, dass die Kinder alle vier Grundrechenarten (Rechenoperationen) beherrschen und ausführen können sollen.
Damit ist nicht gemeint, dass Kinder Aufgaben und Regeln "ohne Verständnis" auswendig lernen sollen. Ziel der ersten Schuljahre ist, dass Kinder Vorstellungen zu den verschiedenen Rechenoperationen erlangen, ein sogenanntes "Operationsverständnis" aufbauen und somit die Kenntnis darüber erlangen, welche Handlung(en) mit der jeweiligen Operation verknüpft sind. Doch was kann man unter Operationsverständnis verstehen?!
Zu einem umfassenden Operationsverständnis gehört die Berücksichtung und Förderung der folgenden drei Aspekte:
Die Entwickung eines umfassenden Operationsverständnisses zu jeder Rechenoperation ist wichtig, um reale Situationen deuten und diese mit einer Rechenoperation in Verbindung bringen zu können. Im Unterricht gibt es nicht selten Kinder, die auch ohne ein umfassendes Verständnis für Operationen ihre Schulzeit durchlaufen und lediglich Regeln und Verfahren "auswendig" lernen und anwenden.
Eigenaktivität
Rechnen Sie zunächst folgende Rechenaufgabe: "3 : ½"
Überlegen Sie sich zu dieser Aufgabe ein passendes Bild oder eine Rechenaufgabe. Was stellen Sie sich vor?
Grundvorstellungen zur Subtraktion
Zur Entwicklung eines umfassenden Operationsverständnisses müssen unter anderem sogenannte Grundvorstellungen zur Rechenoperation aufgebaut werden. Zu jeder Rechenoperation gibt es verschiedene Grundvorstellungen, die mit unterschiedlichen Auffassungen zur Operation verknüpft sind (vgl. Fromme, Wartha & Benz 2011).
Im Folgenden liegt der Fokus auf dem Aufbau des Operationsverständnisses zur Subtraktion.
Von einer "Grundvorstellung zur Subtraktion" im natürlichen Zahlenraum wird immer dann gesprochen, wenn in einem Zahlentripel (Konstellation dreier Zahlen: beispielsweise 3, 5, 8) eine der kleineren Zahlen (Teilmenge) gesucht wird: 8 - 3 = ?, 8 - ? = 3, 3 + ? = 8. ? + 5 = 8, 8 - ? = 5 oder 8 - 5 = ? (vgl. u.a. Selter, Prediger, Nührenbürger & Hussmann 2012; Wessel 2015). Im Gegensatz dazu wird bei Grundvorstellungen zur Addition nach der größten Zahl (Gesamtheit) gefragt: 3 + 5 = ?, 5 + 3 = ?.
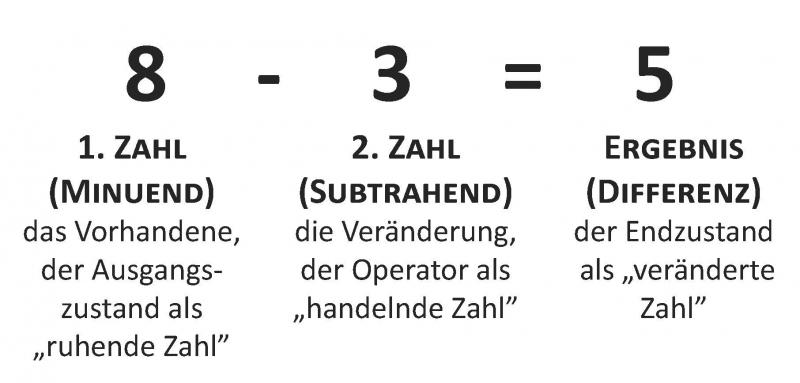
Die Subtraktion wird oft mit "etwas wegnehmen/abgeben/vermindern" oder Ähnlichem in Verbindung gebracht. Viele Kinder verfügen bereits vor Schuleintritt über diese oder eine ähnliche Handlungsvorstellung von Subtraktion, da sie häufig in Spiel- und Alltagssituationen vorkommt und die "natürliche" Umkehrung zur Vorstellung von Addition als "Hinzufügen/Dazutun" verkörpert.
An diese Vorerfahrungen der Kinder mit der Subtraktion knüpfen auch Schulbücher an, indem sie die Subtraktion über die Grundvorstellung des "Abziehens" einführen. Doch ebenso ist es wichtig, den Kindern im Laufe des ersten Schuljahres zu vermitteln, dass die Subtraktion noch mehr ist als nur "Abziehen" (vgl. Wartha & Schulz 2013, S. 32).
Bei der Subtraktion gibt es folgende drei zentrale Grundvorstellungen (vgl. Fromme et al. 2011, S. 36; Padberg & Benz 2011, S. 115):
 Abziehen
Abziehen
6 - 1
Torben möchte sechs Eier zum Frühstück machen. Ein Ei fällt ihm auf den Boden. Wie viele Eier kann er jetzt noch machen?
 Vergleichen 9 - _ = 6 ⇔ 9 - 6
Vergleichen 9 - _ = 6 ⇔ 9 - 6
Jan hat neun Äpfel. Paula hat sechs Äpfel. Wie viele Äpfel hat Jan mehr als Paula?
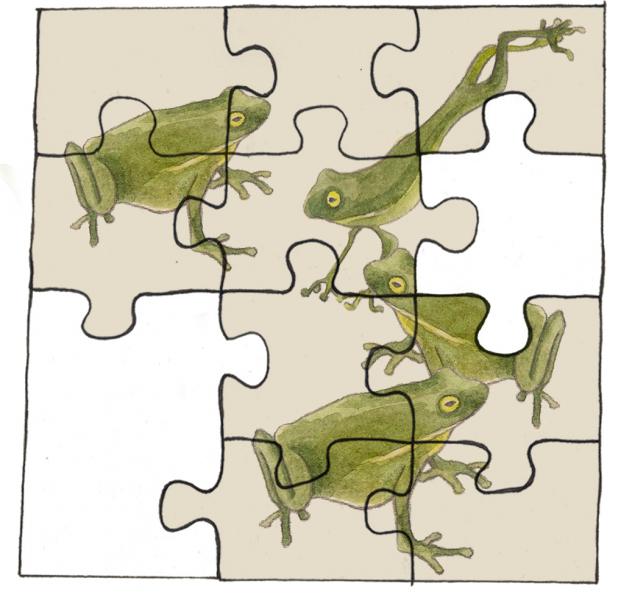 Ergänzen 9 + _ = 12 ⇔ 12 - 9
Ergänzen 9 + _ = 12 ⇔ 12 - 9
Marie hat neun Puzzleteile zusammengesetzt. Das Bild hat insgesamt zwölf Teile. Wie viele Teile fehlen ihr noch?
Das zeigt, dass es verschiedene Lösungwege für Subtraktionsaufgaben gibt. Beim Abziehen wird das Ergebnis durch ein Abziehen des Subtrahenden vom Minuenden bestimmt. Beim Ergänzen wird zur Lösung der Aufgabe vom Subtrahenden zum Minuenden ergänzt, wobei das "Hinzugefügte" das Ergebnis der Aufgabe darstellt. Beim Vergleichen wird das Ergebnis über den Unterschied zwischen der Gesamtheit und einer Teilmenge ermittelt (vgl. Wessel 2015).
Neben diesen drei dargestellten gibt es bei der Subtraktion weitere Grundvorstellungen. Zum Beispiel kann Subtrahieren auch eher statisch gedeutet werden im Sinne des "Enthalten sein" (Es gibt Plättchen in zwei Farben. 2 von 11 Plättchen sind rot. Wie viele sind blau?).

Alle Grundvorstellungen können anhand von lebensweltlichen Situationen, wie beispielsweise beim Sammeln von Kastanien (linke Abbildung), verdeutlicht werden.
Dabei sollte die Eindeutigkeit von Bildern stets hinterfragt werden. Denn Bilder sind immer ein eigener Lernstoff mit möglichen Hürden und können oftmals mehrdeutig interpretiert werden.
Vergleichssituationen zu lösen, fällt Kindern oft schwerer als Situationen des Abziehens oder Ergänzens, so belegen es auch Studien (vgl. u. a. von Stern 1998).
Doch woran liegt das?
Eigenaktivität
Nehmen Sie sich die Zeit und schauen Sie in Ihrem Schulbuchwerk nach, welche Grundvorstellungen zur Subtraktion angesprochen werden.
Was fällt Ihnen auf?
Ein Grund für diese Schwierigkeiten beim Lösen von Vergleichssituationen ist die fehlende oder mindestens nachrangige Thematisierung aller Grundvorstellungen zur Subtraktion in Schulbüchern und damit im Mathematikunterricht.
Ein weiterer Grund ist, dass den Kindern bei Situationen zum "Abziehen" oder "Ergänzen" in den Aufgabenformulierungen konkrete Handlungsanweisungen gegebenen werden, wie z. B.
-
"Wenn ich drei Kastanien wegnehme, wie viele bleiben übrig?"
-
"Wie viele Kastanien müsste ich noch bekommen/abgeben, damit wir gleich viele haben?"
Die Kinder können diese Handlung konkret am Material oder mental im Kopf durchführen. Bei Situationen zum "Vergleichen" fehlt dieser Hinweis in der Aufgabenformulierung. Die Kinder stehen vor der Herausforderung, die Begrifflichkeiten "mehr" und "weniger" inhaltlich zu verstehen.
Tipp: Sie können eine Vergleichsaufgabe "Wie viele Kastanien habe ich mehr/weniger?" zu Beginn der Thematisierung als Hilfestellung für die Kinder in eine Ergänzungsaufgabe umformulieren: "Wie viele Kastanien muss ich bekommen/abgeben, um gleich viele zu haben?". Wichtig ist dabei die Verknüpfung beider Vorstellungen mit der Subtraktion.
Fähigkeit zum Darstellungswechsel
Für ein umfassendes Operationsverständnis sind Grundvorstellungen zur Rechenoperation bedeutsam, die durch die Vernetzung aller Darstellungsformen über konkrete Handlungen erworben werden. Demnach sind für den Aufbau des Operationsverständnisses vielfältige Darstellungswechsel notwendig.
Welche Darstellungsformen gibt es?
In dieser kommentierten Powerpoint-Präsentation wird gezeigt, welche Darstellungsformen es gibt und wie diese miteinander verknüpft sind.

Die verschiedenen Darstellungsformen (Handlung, Bild, Sprache, Mathesprache) können nicht alleinig durch ihre Präsenz ein Operationsverständnis erzeugen, denn die Rechenoperation kann nicht "gesehen" werden, sondern muss immer erst in die entprechende Darstellungsform hineininterpretiert werden.
Zum Operationsverständnis gehört demnach die Fähigkeit, Verbindungen zwischen allen Darstellungsformen zu einer Rechenaufgabe herstellen zu können. Dabei stellen diese Wechsel, also das "Übersetzen" zwischen den verschiedenen Darstellungsformen, einen komplexen Prozess dar. Die Darstellungsformen müssen immer wieder verglichen werden und sind keinesfalls als "Einbahnstraßen" zu verstehen. Die Kinder sollen "netzartige Geflechte" entwickeln mit dem Ziel, zwischen den verschiedenen Darstellungen flexibel hin- und herübersetzen zu können.
Die Aufgabe "Wie viele Äpfel hat Jan mehr als Paula?" kann durch Nachspielen der Situation, also innerhalb der Darstellungsform "Handlung" (durch eine "Eins-zu-Eins-Zuordnung" und anschließendem Abdecken/Wegschieben von Äpfeln/Plättchen), gelöst werden, durch das Anfertigen eines passenden Bildes und/oder durch das Übersetzen in die Rechenaufgabe "9 - 6".
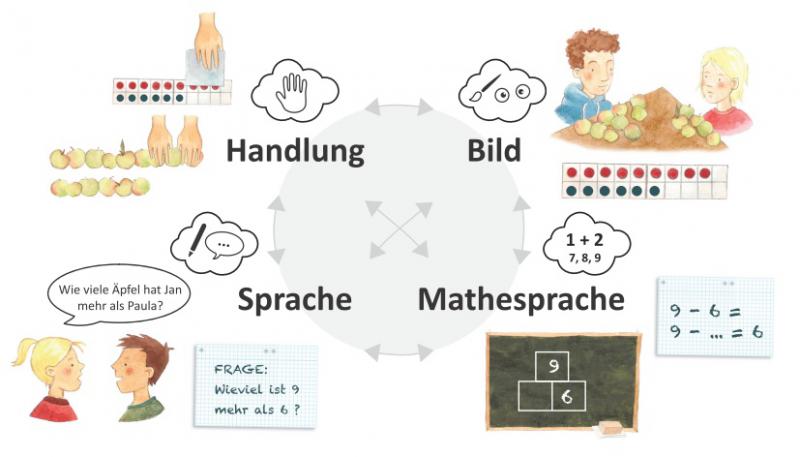 (in Anlehnung an PIK AS 2016a und Kuhnke 2013)
(in Anlehnung an PIK AS 2016a und Kuhnke 2013)
Vermutlich haben Sie die Übersetzungen zwischen den verschiedenen Darstellungsformen bereits verinnerlicht, gar "automatisiert" und nehmen diese gar nicht mehr so bewusst wahr. Dem Kind sind diese für uns "einfachen" Darstellungswechsel keinesfalls unmittelbar klar und stellen eine große Herausforderung dar. Denn für das Kind ist es ein Unterschied, ob eine Aufgabe als konkrete Sachsituation, als Bild oder symbolisch als Rechenaufgabe vorliegt.
Wenn ein Kind die "Apfelaufgabe" mit Äpfeln mit Hilfe von Plättchen oder gezeichneten Kreisen löst, dann hat das für das Kind möglicherweise nichts mit der Rechenaufgabe "9 - 6" zu tun. Und wenn man dem Kind sagt, dass es die Aufgabe "9 - 6" lösen kann, indem es von der Zahl 9 um 6 Schritte zurückzählt, dann verknüpft das Kind diese Zählhandlung vermutlich weniger mit der Sachsituation, denn schließlich kann das Zählen "mechanisch" durchgeführt werden ohne jede Vorstellung von einem konkreten Kontext.
„Kinder scheitern bei 'Übersetzungsprozessen', wenn sie nicht verstehen, was sie tun" (Hess 2012, S. 201).
Von großer Bedeutung für den Aufbau eines Operationsverständnisses ist das Handeln an geeignetem didaktischen Material (siehe auch: Material). Deswegen ist es wichtig, dass Kinder Zahlen und Mengen am Material strukturiert darstellen können, z. B. am Zwanzigerfeld oder an Rechenketten.
Letztendlich muss sich jedes Kind selbst sein eigenes Operationsverständnis aufbauen. Deswegen ist es wichtig, Übersetzungen zwischen allen Darstellungsformen bewusst zu fördern und mit den Kindern zu klären, wann und warum eine Darstellungsform "passt". Dafür gibt es Aktivitäten im Unterricht, die diesen Prozess unterstützen können (vgl. Häsel-Weide 2014). Eine Beispielaktivität - "Minustrio" - finden Sie im Unterrichtsteil.
Erkennen und Nutzen von Beziehungen und Strukturen zwischen Aufgaben
Ein umfassendes Operationsverständnis zeigt sich schließlich auch darin, Beziehungen und Strukturen zwischen Aufgaben entdecken, nutzen und beschreiben zu können.
Eigenaktivität
Schaunen Sie sich das KIRA-Video an, in dem Lina die Aufgabe 5 - 2 löst.
Welche Beziehung nutzt Lia aus?
Der Zusammenhang zwischen Addition und Subtraktion (als Umkehroperation) ist wichtig für ein umfassendes Operationsverständnis der Subtraktion.
Kinder sollten die Ergebnisse der Minusaufgaben sicher mit Hilfe der Beziehung zu den entsprechenden Plusaufgaben und anderen halbschriftlichen Rechenstrategien ableiten können.
Dafür brauchen sie
-
ein gesichertes Teile-Ganzes-Verständnis (Tipp: Schauen Sie sich die Seite Zahlvorstellung an.)
-
die gedächtnismäßige Verfügung über sogenannte Zahlentripel (7/5/12; 7 + 5 = 12; 12 - 5 = 7)
-
und die Grundvorstellung der Subtraktion als "Ergänzen" (vgl. PIK AS 2016b)
Durch geeignete Übungsformate, wie beispielsweise Entdecker-Päckchen (Tipp: Schauen Sie sich die Seite
Üben an.), können Kinder angeregt werden, Beziehungen und Strukturen zwischen Aufgaben zu entdecken und auszunutzen. Die Kinder sollten im Laufe der Grundschulzeit folgende geschickte, nicht-zählenden Rechenstrategien entwickeln:
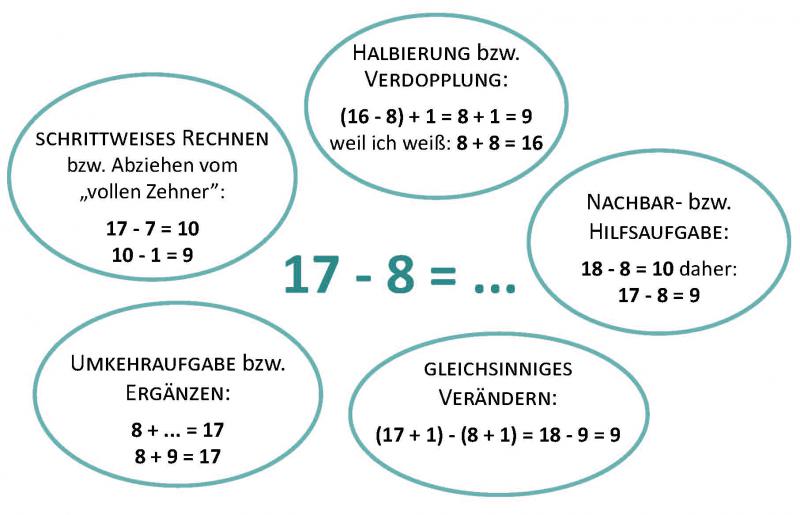
Aufgrund der engen Verbundenheit beider Rechenoperationen wird die Subtraktion im Anfangsunterricht immer häufiger fast gleichzeitig mit der Addition eingeführt (vgl. Hasemann & Gasteiger 2014, S. 92).
Das Übertragen von Rechenregeln der Addition auf die Subtraktion sind eine mögliche Schwierigkeit im Unterricht, da die von den Kindern bereits entdeckten Rechengesetze der Addition nicht automatisch für die Subtraktion gelten. Es kommt häufig vor, dass Kinder folgende "Operationseigenschaft" der Addition auf die Subtraktion übertragen: das Kommutativgesetz (4 + 3 = 3 + 4).
Die Kinder müssen inhaltlich verstehen, warum die Rechenregel - in diesem Fall das Vertauschen der Zahlen bei der Subtraktion (7 - 5 ist nicht das gleiche wie 5 - 7) - "nicht geht" und es nicht einfach auswendig lernen, dass es eben "verboten" ist, die Zahlen zu vertauschen.
Es ist wichtig, diese Operationseigenschaften mit Hilfe anderer Darstellungsformen zu veranschaulichen, beispielsweise indem passende Handlungen (Rollenspiele) zu Aufgaben durchgeführt werden:
So können von sieben Äpfeln problemlos fünf Äpfel abgegeben werden, dann bleiben noch zwei Äpfel übrig. Doch wenn man von fünf vorher eingesammelten Äpfeln sieben Äpfel abgeben möchte, fehlen noch zwei Äpfel, um sie überhaupt weggeben zu können.
Hier und im Materialteil finden Sie eine Übersichtstabelle über die Operationseigenschaften der Subtraktion.
Operationseigenschaften der Subtraktion
Zusammenfassung
Es lässt sich resümieren, dass es das Ziel sein muss, Kindern ein umfassendes Operationsverständnis zu ermöglichen, indem alle drei Aspekte "Grundvorstellungen", "Darstellungswechsel" und "Beziehungen und Strukturen zwischen Aufgaben" berücksichtigt und gefördert werden.
Die Kinder sollen die Subtraktion in unterschiedliche Situationen und verschiedenen Darstellungsformen hineinsehen können und wissen, wann "Minus" gerechnet werden muss. Dabei sollten Lehrende immer genau überlegen, welche Grundvorstellungen womit verfolgt werden und sensibel sein für die bereits existierenden Individualvorstelllungen der Kinder.
Eine große Herausforderung für Kinder stellen Übersetzungen zwischen den verschiedenen Darstellungsformen dar. Daher liegt der Fokus im Unterrichtsteil auf einer möglichen Aktivität zur Förderung des Darstellungswechsels.