Zahlenketten im Unterricht – zur Förderung inhalts- & prozessbezogener Kompetenzen
Wie Sie im mathematischen Hintergrund schon erfahren haben, bietet das Aufgabenformat der Zahlenketten vielfältige Entdeckungsmöglichkeiten. Wie alle Folgen verfügen sie über „interessante Eigenschaften, die immer wieder Anlass zu neuen Entdeckungen geben, durch die Beschäftigung mit ihnen lassen sich wichtige Arbeits- und Denkweisen entwickeln“ (Weigand 1998, S. 4).
Es lassen sich inhaltsbezogene Kompetenzen fördern. Aber auch – und vor allem wenn es um Entdeckungen, Erläuterungen und Begründungen geht – das Fordern und Fördern der prozessbezogenen Kompetenzen bietet sich durch ein solches Aufgabenformat in besonderer Weise an.
Im Weiteren werden Aufgaben zu fünfgliedrigen Zahlenketten für eine dritte Klasse vorgestellt, die aber sicherlich auch für niedrige Klassen- und Leistungsstufen auf viergliedrige und für leistungsstärkere Kinder auf sechsgliedrige Zahlenketten adaptiert werden können. Gerade das operative Verändern der Zahlenketten bietet viel Raum, um auch die prozessbezogenen Kompetenzen zu fordern und zu fördern.
Im Weiteren werden folgende Sequenzen vorgestellt:
Kennenlernen der Aufgabenvorschrift und mit dem Aufgabenformat vertraut werden
-
Ziel: Kennenlernen der Bildungsregeln
Wie jedes neue Aufgabenformat müssen auch die Zahlenketten zunächst eingeführt werden.
Die Bildungsregeln der Zahlenketten müssen den Kindern deutlich werden, bevor sie in die Arbeit mit dem Aufgabenformat sinnvoll einsteigen können. Dazu macht es auch – vor allem für die spätere Kommunikation über die Zahlenketten – Sinn, mit den Kindern einen Wortspeicher (siehe auch Sprachförderung) zu erarbeiten. Welche Positionen brauchen Namen, um die Gespräche zu vereinfachen? Welche Satzanfänge oder -bausteine erleichtern den Kindern die Arbeit mit den (folgenden) Aufgaben?
Es gibt unterschiedliche Möglichkeiten ein solches Aufgabenformat neu einzuführen, sofern Ihre Schülerinnen und Schüler noch nicht mit den Zahlenketten gearbeitet haben. Überlegen Sie sich, wie Sie die Bildung erklären wollen. Christoph Selter erklärt es so: „Eine Vierer-Zahlenkette wird wie folgt gebildet: Man wählt zwei Startzahlen, schreibt sie nebeneinander und notiert rechts daneben deren Summe. Daneben schreibt man die Summe aus der zweiten und der dritten Zahl als Zielzahl rechts daneben, also zum Beispiel … 2 10 12 22 oder 8 4 12 16“ (Selter o.J., S. 1). Sie wissen am besten, welche Begriffe Ihre Klasse kennt und welche Sie somit nutzen können (z.B. Summe).
Zur Sicherung, dass alle Kinder die Bildungsregel verstanden haben berechnen Sie dann mit allen Kindern gemeinsam einige weitere Zahlenketten. Diese können sowohl halb gefüllt als auch ganz leer sein, sodass Ihre Klasse Vorschläge machen kann.
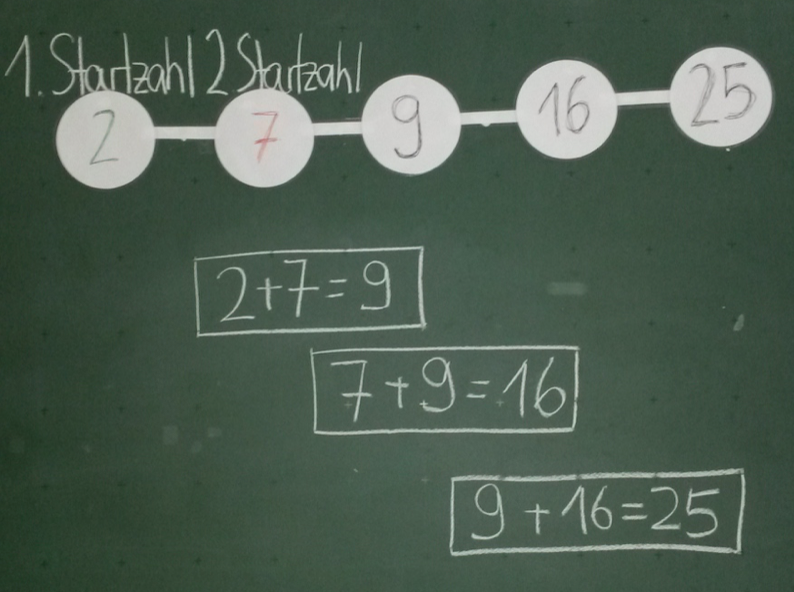
-
Ziel: erstes Rechnen mit den Zahlenketten, um mit dem Aufgabenformat vertraut zu werden
Im zweiten Schritt ist es wichtig, dass die Kinder mit dem Aufgabenformat vertraut werden. „Eine erste Aktivität für beliebige Klassenstufen könnte sein, eigene Zahlenketten zu wählen und zu berechnen“ (Krauthausen & Scherer 2011, S. 5). Bevor Sie Ihre Klasse zu Entdeckungen von mathematischen Besonderheiten und Strukturen heranführen, sollten die Schülerinnen und Schüler Zeit und Raum bekommen, um sich mit dem Aufgabenformat vertraut zu machen. Die Kinder erlangen eine Sicherheit im Umgang mit dem Aufgabenformat. Dabei können sie auch schon erste Einsichten in die Strukturen erlangen – müssen es aber nicht.
Hierzu können zum einen teilweise ausgefüllte Zahlenketten verwendet werden. Die Lücken, die die Kinder berechnen sollten, können dabei auch variieren. Und je nachdem welche Lücken gelassen werden, ist die Bestimmung der fehlenden Zahlen deutlich anspruchsvoller.
Es ist aber auch durchaus sinnvoll, den Kindern leere Zahlenketten zu geben, die sie dann selbstständig ausfüllen können. Dadurch wird eine quantitative Differenzierung – also über die Anzahl der berechneten Zahlenketten – sowie qualitative Differenzierung – also im Sinne eines tieferen Einsteigens in die Muster und Strukturen der Zahlenketten oder beispielweise einen höheren Zahlenraum – ermöglicht (vgl. Krauthausen & Scherer 2011, S. 5).
Operatives Verändern der Startzahlen
Nachdem sich die Kinder mit dem Aufgabenformat beschäftigt haben und ein sicherer Umgang mit den Rechenvorschriften der Zahlenketten sichergestellt wurde, können die operative Veränderungen der Startzahlen die Kinder zu Entdeckungen animieren.
1. Verändeurng der ersten Startzahl
Ziel:
-
Erkennen der Zusammenhänge und Beziehungen zwischen der ersten Startzahl und der Zielzahl.
Darum geht es:
In der ersten Einheit zu den Veränderungen der Startzahlen geht es vor allem darum, dass die Kinder erste Entdeckungen zu den Strukturen der Zahlenketten anstellen.
Eine Möglichkeit besteht in der Erhöhung der ersten Startzahl um 1. Durch eine systematische Erhöhung der ersten Startzahl um 1 und den Arbeits- bzw. Forscherauftrag „Wie verändert sich die Zielzahl, wenn die erste Startzahl um 1 größer wird?“ werden die Kinder angeleitet, Muster und Strukturen des Aufgabenformates zu erkennen.
Mögliche Knackpunkte:
Aber nicht nur das Erkennen von Strukturen, sondern auch das Begründen oder das Darstellen dieser Zusammenhänge kann hier gefördert werden.
„Warum ist das so?“ sollte die Kinder dazu anleiten, ihre Entdeckungen zu beschreiben. (Zur Erinnerung, bei einer fünfgliedrigen Zahlenkette, erhöht sich die Zielzahl um 2, wenn die erste Startzahl um 1 erhöht wird).
Dazu können die Kinder sowohl Forschermittel, als auch die Begriffe aus dem Wortspeicher zur Beschreibung nutzen. Als Anschauung für die Veränderung, kann in die betreffenden Kreise eine kleine „+1“ gezeichnet werden, oder die Kinder legen immer ein Plättchen in die Felder. Sie wissen am besten, welche Möglichkeiten in Ihrer Klasse zur Verfügung stehen.
2. Veränderung der zweiten Startzahl
Ziel:
Darum geht es:
Analog zur Erhöhung der ersten Startzahl, wird in der nächsten Unterrichtseinheit die zweite Startzahl sukzessive um 1 erhöht. Die Arbeitsaufträge „Wie verändert sich die Zielzahl, wenn die erste Startzahl um 1 größer wird?“ und „Warum ist das so?“ können ebenfalls beibehalten werden.
Mögliche Knackpunkte:
Auch hier noch einmal kurz zur Erinnerung: Da die zweite Startzahl dreimal in die Zielzahl eingeht, wirkt sich die Erhöhung der zweiten Startzahl dreifach auf die Zielzahl aus. Lassen Sie also die Kinder zu Beginn dieser Einheit vielleicht erst einmal eine Vermutung aufschreiben, was sie glauben, wie sich die Zielzahl verändert, wenn die zweite Startzahl um 1 erhöht wird. Diese Vermutung kann dann anhand von Beispielen überprüft. Darauf können die Schülerinnen und Schüler Folgerungen ableiten und Begründungen geben. Dies entspricht der prozessbezogenen Kompetenz des Argumentierens.
Hierzu bietet sich für die Durchführung auch eine Gruppenarbeit nach der dem Ich-Du-Wir-Prinzip an.
3. Gleichzeitige Veränderung beider Startzahlen
Ziel:
-
Erkennen der Zusammenhänge und Beziehungen beider Startzahlen mit der Zielzahl.
Darum geht es:
Auch die Erhöhung beider Startzahlen leitet die Kinder zu Entdeckungen an und ist folglich eine weitere Möglichkeit mit dem Aufgabenformat Zahlenketten auch die prozessbezogenen Kompetenzen zu fördern. Hierbei können die Kinder auch auf die Erkenntnisse aus den vorherigen Aufgaben zurückgreifen und auch zunächst Vermutungen anstellen. Da die Erhöhung der ersten Startzahl um 1 eine Erhöhung der Zielzahl um 2 und die Erhöhung der zweiten Startzahl um 1 eine Erhöhung der Zielzahl um 3 bewirkt, bewirkt also die gleichzeitige Erhöhung beider Startzahlen um 1 eine Erhöhung um 5.
Die Arbeitsausträge können dabei ebenfalls identisch bleiben.
4. Verallgemeinern der Entdeckungen
Ziel:
-
Übertragen der Entdeckungen auf eine allgemeingültige Darstellung und treffen von verallgemeinerten Aussagen.
Darum geht es:
Der Einblick in die Zusammenhänge und Beziehungen bzw. die Strukturen ist bei der Bearbeitung weiterer Aufgaben im Kontext der Zahlenketten wichtig (vgl. Verboom 1998, S. 9). Doch nicht nur in Bezug auf dieses Aufgabenformat ist eine Verallgemeinerung sinnvoll – so zeigt Kathrin Akinwunmi: Verallgemeinern „nimmt einen wichtigen Stellenwert in der Entwicklung des algebraischen Denkens ein und stellt gleichzeitig einen Anknüpfungspunkt für die Erarbeitung von Variablenkonzepten in der Sekundarstufe dar“ (Akinwunmi 2012, S. 284) (siehe auch Spiralprinzip). Studien zeigen, dass Schülerinnen und Schüler der Sekundarstufe im Umgang mit Variablen Schwierigkeiten aufweisen (vgl. ebd., S. 277).
Eine altersgemäße Möglichkeit die Entwicklung des algebraischen Denkens zu fördern besteht in der Verallgemeinerung der Zusammenhänge in einer Zahlenkette.
So schlägt Verboom (1998) vor, die fünf Zahlen auf bunten Perlen zu notieren und zu sagen, dass einige dieser Perlen verschwunden sind und nun alle Zahlen mit den ersten beiden dargestellt werden sollen. Dabei kann ein solches Bild entstehen:

Eine weitere Möglichkeit wäre, den Kindern kleine Säckchen zu zeigen, in die man eine unbekannte Anzahl an Plättchen/Mugelsteinen/Perlen steckt. Und dann zu erläutern, dass das eine (blaue) Säckchen die erste Startzahl ist und das grüne Säckchen für die zweite Startzahl steht. Mit dem Auftrag „Versuche alle Zahlen der Zahlenkette mit den Säckchen für die beiden Startzahlen darzustellen.“

Auch die Entdeckungen in den vorangegangenen Aufgaben lassen sich so verallgemeinert darstellen:

So sieht man hier beispielsweise, dass, wenn die erste Startzahl um 1 erhöht wird, sich die Zielzahl um 2 erhöht. Denn beide Säckchen haben jeweils ein Plättchen hinzuerhalten. Und das ist unabhängig von der Zahl, die sich hinter der ersten Startzahl verbirgt. Somit kann die Verallgemeinerung „Wenn die erste Startzahl sich um eins erhöht, erhöht sich die Zielzahl um 2.“ veranschaulicht werden.
Um beim Argumentieren und Begründen allgemeine Aussagen treffen zu können, wird eine solche Darstellung für die Kinder hilfreich sein.
Zahlenketten zu gegebenen Zielzahlen finden
Nach der Thematisierung der Veränderungen der Zielzahlen und der Verallgemeinerung können die Kinder in der abschließenden Einheit nun alles erworbene Wissen nutzen, um möglichst viele Zahlenketten zu einer bestimmen Zielzahl zu finden. Dabei ist wichtig, dass Sie nicht eine zu große Zielzahl wählen, damit für die Kinder auch die Möglichkeit besteht alle finden zu können.
-
Ziel: Nutzen der Einsichten über Zusammenhänge und Strukturen der Zahlenketten, um ein systematisches Vorgehen der Kinder zu fördern
„Finde möglichst viele Zahlenketten zur Zielzahl 50. Beschreibe wie du vorgegangen bist.“ eignet sich sehr gut, um zunächst alle Kinder zum Lösen der Aufgabe anzuregen. Alle Kinder können diese Aufgabe lösen.
Mögliche Knackpunkte:
Sollten Sie Schülerinnen und Schüler haben, die hier noch sehr lange unsystematisch ausprobieren, so könnten Sie Tippkarten bereithalten, die an die Entdeckungen aus den vorherigen Stunden erinnern. Auch eine Visualisierung der gemeinsam erarbeiteten Verallgemeinerung ist eine Möglichkeit, um die Kinder zu systematischem Vorgehen anzuleiten.
In einer zweiten Phase können die Kinder in Kleingruppen zusammenkommen und ihre gefundenen Lösungen – und Lösungsstrategien – vergleichen. Der weitere Forscherauftrag „Habt ihr alle gefunden? Und warum seid ihr sicher, dass ihr alle gefunden habt? Begründet!" leitet die Kinder noch einmal zum Strukturieren der Lösungen an.
Hier können die Kinder auch andere Darstellungen nutzen als die Zahlenketten. Manche benötigen diese vielleicht noch als Visualisierung, andere können die Werte für die erste und die zweite Startzahl auch schon in einer Tabelle notieren. Die Kinder können auch eigene Wege finden, das für sich übersichtlich zu notieren. Verweisen Sie auch auf Möglichkeiten zur Darstellungen von Zusammenhängen, beispielweise durch Pfeile (siehe Forschermittel).
Weiterführende Möglichkeiten: Muster und Strukturen für Aufgabenadaptionen und -veränderungen nutzen
Bei all den Aufgaben zur systematischen Veränderung der Startzahlen liegen die mathematischen Strukturen den Entdeckungen zugrunde. „An dieser Stelle zeigt sich auch, wie sinnvoll und notwendig die Erkundung durch die Lehrerin selbst ist“ (Scherer 1997, S. 38). So können Sie nun das Aufgabenformat der Zahlenketten an Ihre Lerngruppe und an Ihren Unterricht anpassen und sicher auf Schülerfragen und -lösungen eingehen. Die Handlungswirksamkeit für den eigenen Unterricht nimmt deutlich zu.
Es sind noch deutlich mehr Aufgabenstellungen zu den Zahlenketten möglich als die hier dargestellten. Eine Unterrichtsreihe zu Zahlenketten kann beliebig erweitert werden. Was ist das besondere an der Zielzahl, wenn man zwei identische Startzahlen wählt? Was passiert mit der Zielzahl, wenn man die beiden Startzahlen vertauscht? Solche und weitere Fragen können ebenfalls behandelt werden. Überlegen Sie selbst, was sich noch anbietet.
Weitere Anregungen können Sie sich auch im Forscherheft vom Partnerprojekt PIKAS holen, bei dem es neben den operativen Veränderungen der Startzahlen noch weitere Aufgaben rund um das Aufgabenformat der Zahlenketten gibt. Eine Verlinkung dazu finden Sie im Material.