Prozessbezogene Kompetenzen fördern
Wie im Hintergrund verdeutlicht, sind Zahlenmauern leicht verständlich und einfach herzustellen. Sie ermöglichen vermischte Additions- und Subtraktionsaufgaben und damit die Übung grundlegender Rechenfertigkeiten. Zu ein und derselben Grundsituation lässt sich eine Fülle von Fragestellungen (z.B. auch durch operative Veränderung wie die Erhöhung des linken Basissteines jeweils um 1.) finden, die ohne großen Aufwand im Sinne einer natürlichen Differenzierung bearbeitet werden können. Dabei sind unterschiedliche Lösungen und Lösungsstrategien - z. B. flexible halbschriftliche Vorgehensweisen (vgl. Krauthausen 1993 & 1995) - möglich, so dass sich die Übungen problemlos den individuellen Leistungsmöglichkeiten der Kinder anpassen.
Auf dieser Seite wird folgender Punkt thematisiert:
-
Wie können Zahlenmauern im Unterricht eingesetzt werden?
Darstellung einer möglichen Unterrichtseinheit
1. Lernvoraussetzungen erkunden bzw. schaffen
Die Schüler und Schülerinnen sollten sowohl die Addition als auch die Subtraktion und Ergänzungsaufgaben verstehen (d.h. sie sollten bereits über ein Operationsverständnis verfügen). Zudem sollten sie wissen, wie sie Additions-, Subtraktions- und Ergänzungsaufgaben lösen können. Und wenn sie in den Bereichen noch Schwierigkeiten haben, sollten sie zumindest in der Lage sein, die Aufgaben mit entsprechenden Hilfsmitteln zu lösen. (Bsp.: Welches Material kann mir helfen? Wo steht das Material im Klassenraum? Wie nutze ich das Material richtig und sinnvoll?)
2. Einstieg - Vorstellen des Übungsformats
Ist das Aufgabenformat den Schülerinnen und Schülern noch unbekannt, kann man die Struktur einer Zahlenmauer an einer Dreiermauer mit einfachen Zahlenwerten erklären.
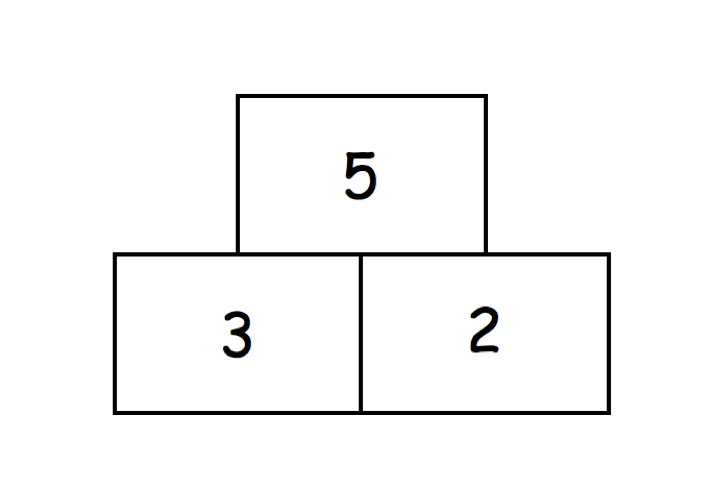
Auf diese Weise spielen die Rechenfertigkeiten nur eine untergeordnete Rolle. Denn bevor ein Aufgabenformat in Übungskontexten eingesetzt werden kann, stellt es zunächst selbst einen Lernstoff dar.

Versammeln Sie Ihre Lerngruppe im Sitzkreis vor der Tafel und füllen Sie das erste Feld aus. Lassen Sie Ihre Schülerinnen und Schüler vermuten, wie die weiteren Felder ausgefüllt werden müssen (stummer Impuls). In der Regel durchschauen die Kinder das Prinzip sehr schnell; spätestens bei einer zweiten Zahlenmauer.
Das Verständnis für die Aufbauregel ist wesentlich für die weitere Arbeit mit diesem Aufgabenformat. Vergewissern Sie sich, dass alle Schülerinnen und Schüler das Prinzip verstanden haben. Prüfen Sie das nach, indem Sie auch größere Zahlenmauern einsetzen bzw. Zahlenmauern, die unvollständige Basissteine haben und somit auch die Subtraktion zur Lösungsfindung einbezogen werden muss. Ein Prüfstein kann helfen, dass die Schülerinnen und Schüler selbst einschätzen können, ob eine Zahlenmauer korrekt gelöst wurde oder nicht.
Dazu eignen sich unter anderem folgende Aufgabenstellungen:
Die Basisreihe ist komplett vorgegeben, gesucht ist der Deckstein.
Einige Steine (und zwar in verschiedenen Zeilen) sind vorgegeben, die restlichen Steine sind zu berechnen.
Wie die beiden Aufgaben zuvor, aber mit verschieden hohen Mauern (Anzahl der Basissteine).
Die Kinder entsprechend ihrer bereits erarbeiteten Zahlenräume selbstständig Zahlen wählen und diese rechnen lassen.
3. Erarbeitung
Zum Durchdringen der Muster und Strukturen der Zahlenmauern bieten sich unterschiedliche Aufgabenstellungen an – die sicherlich auch unterschiedliche Schwerpunkte setzen und zu verschiedenen Entdeckungen anregen. Die Tabelle im Folgenden gibt eine Übersicht darüber, was sich im Kontext der Zahlenmauern zur Förderung der prozessbezogenen Kompetenzen anbietet. Dabei handelt es sich um Unterrichtseinheiten, die häufig ein bis zwei Unterrichtsstunden umfassen können und hier übersichtsartig angeordnet sind und somit eine Anregung zur Umsetzung darstellen. Im Anschluss wird ein Beispiel detailliert betrachtet.
Folgende Aufgabenbeispiele nehmen systematische Veränderungen in den Zahlenmauern in den Blick. Dabei steht weniger das Rechnen im Vordergrund als vielmehr eine Förderung der Prozessbezogenen Kompetenzen Problemlösen, Darstellen oder Kommunizieren. Natürlich ist das sichere Ausrechnen eine Basis dafür, die operativen Veränderungen und ihre Auswirkungen untersuchen zu können. Eine Hürde für so manches Kind mit Schwierigkeiten beim Rechnen. Daher kann der Zahlenraum auch sehr klein gewählt werden, wenn das ansonsten eine Schwierigkeit für die Schülerinnen und Schüler darstellt.
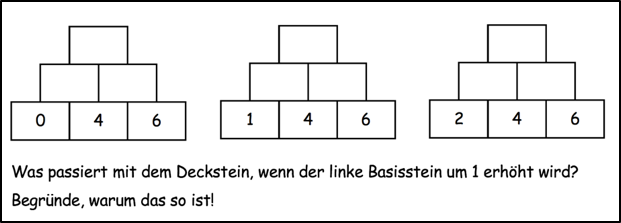
Man verändere einen der äußeren Basissteine (zunächst um ±1, dann auch um andere Werte).
Welche Auswirkungen hat es auf die Zahl im Deckstein?
Hierbei ist es vor allem wichtig, dass die Kinder zum Entdecken sowie Beschreiben und Begründen angeregt werden.
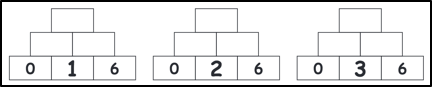
Man verändere den mittleren Basisstein (zunächst um ±1, dann auch um andere Werte).
Welche Auswirkungen auf die Zahl im Deckstein?
Vor allem in Verbindung mit der vorherigen Aufgabe bietet dieses Aufgabenstellung Potential mit den Kindern zunächst Vermutungen anzustellen, was mit dem Deckstein passiert, wenn der mittlere Basisstein (um 1) erhöht wird. Hierbei ist dann auch das Vermuten, Überprüfen und Begründen besonders.
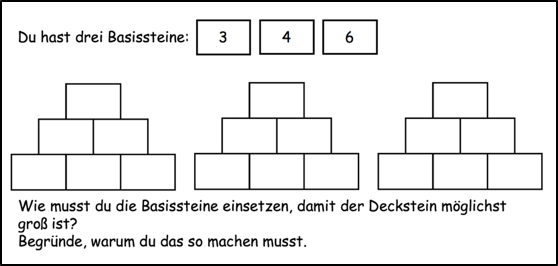
Durch die Variation der Basissteine sollen die Kinder dazu angeleitet werden, zu erkennen, dass die größte Zahl im mittleren Bassisstein stehen muss, um die größte Zahl im Deckstein zu haben. Die beiden äußeren Basissteine können dabei aber vertauscht werden, da beide einmal in den Deckstein eingehen und deren Position am Ergebnis nichts ändert.

Die Zahl im Deckstein soll (un-)gerade sein! Welche Eigenschaften müssen die Basissteine haben?
Nun soll das Beispiel „Finde möglichst viele Zahlenmauern mit dem Deckstein 5.“ genauer betrachtet werden:
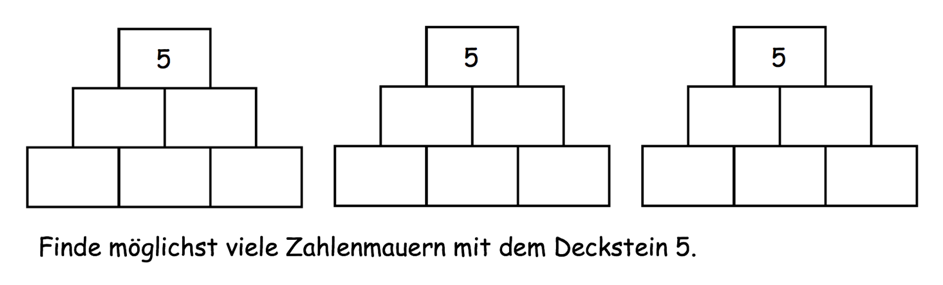
Insgesamt gibt es also 12 mögliche Zahlenmauern:
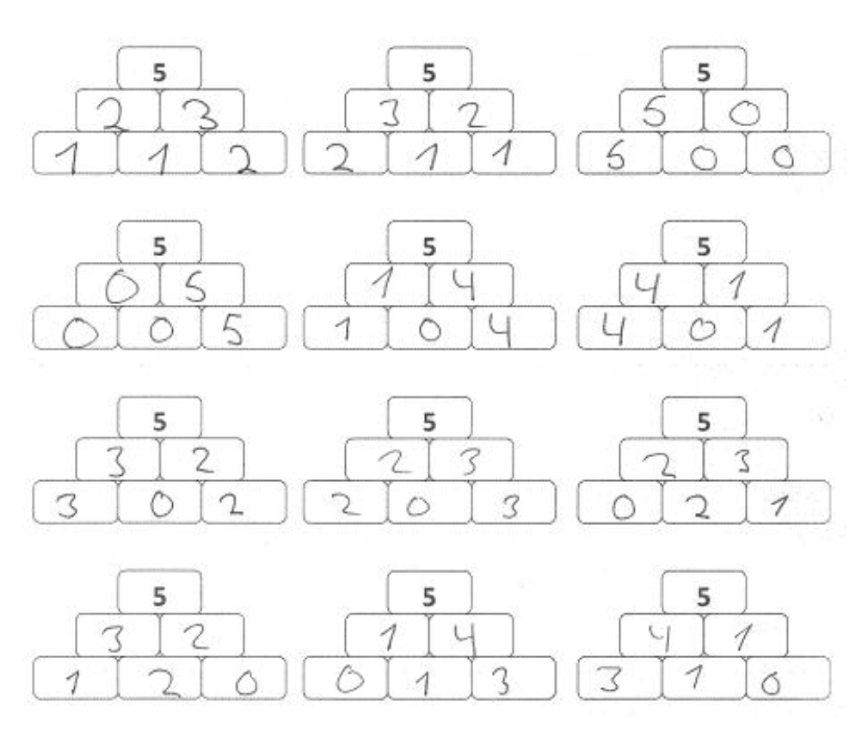
Die erste Möglichkeit liegt darin, in den Mittelsteinen die Aufgabe 5+0 zu wählen. Daraus resultiert für die Basissteine nur eine einzige Möglichkeit.
Zudem kann hier auch noch die Tauschaufgabe angegeben werden.
Die zweite Möglichkeit besteht darin, als Werte für die Mittelsteine die Aufgabe 4+1 zu wählen.
Daraus resultieren für die Basissteine zwei Möglichkeiten.
Bzw. 4, wenn die Tauschaufgaben berücksichtigt werden.
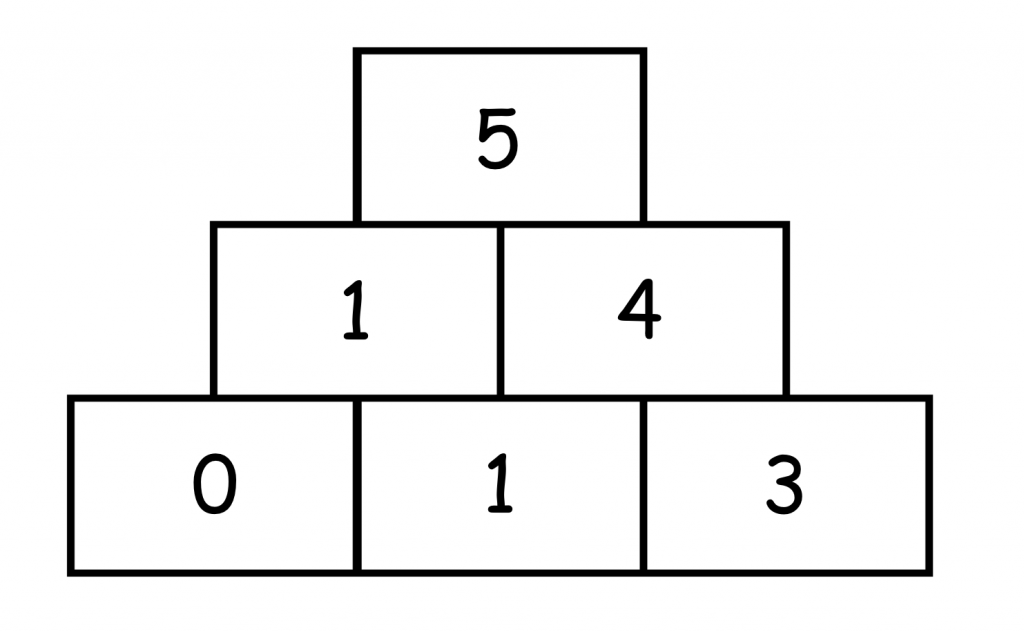
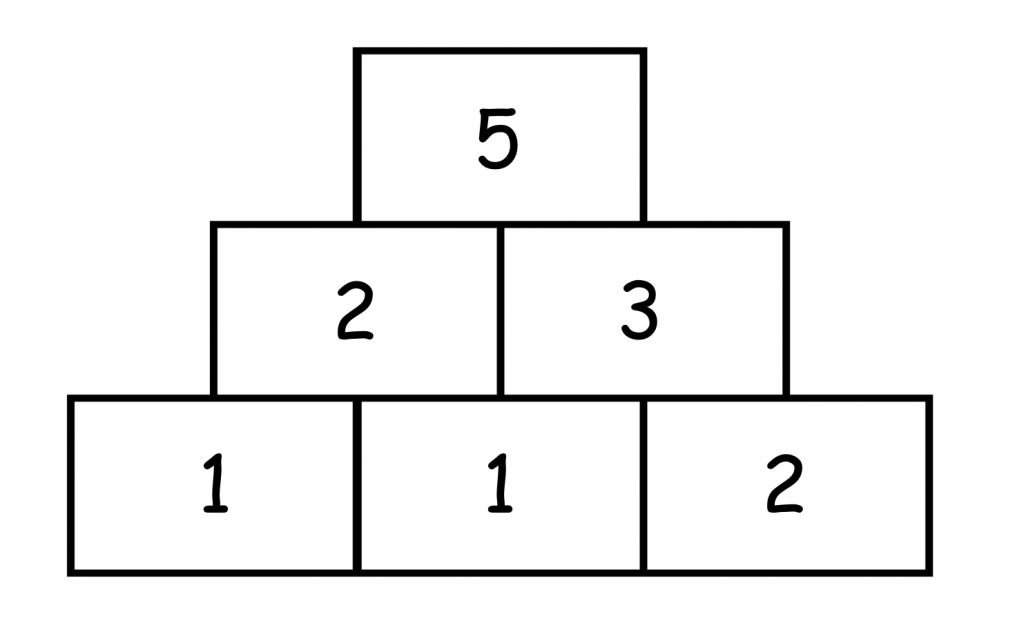
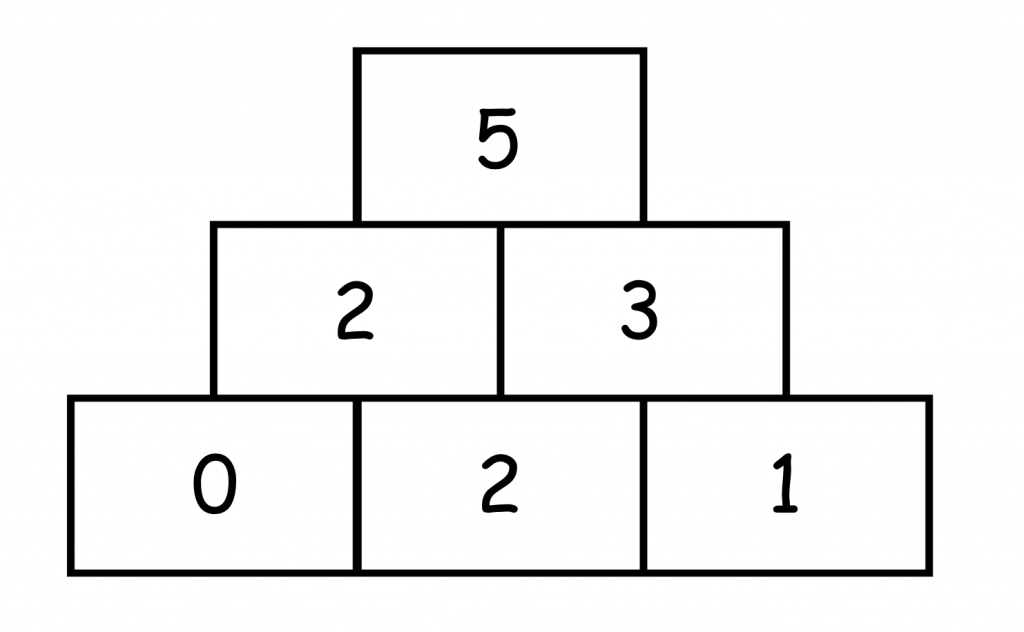
Die letztmögliche Zerlegung der Mittelsteine ist die Aufgabe 3+2.
Daraus resultieren für die Basissteine sogar drei Möglichkeiten.
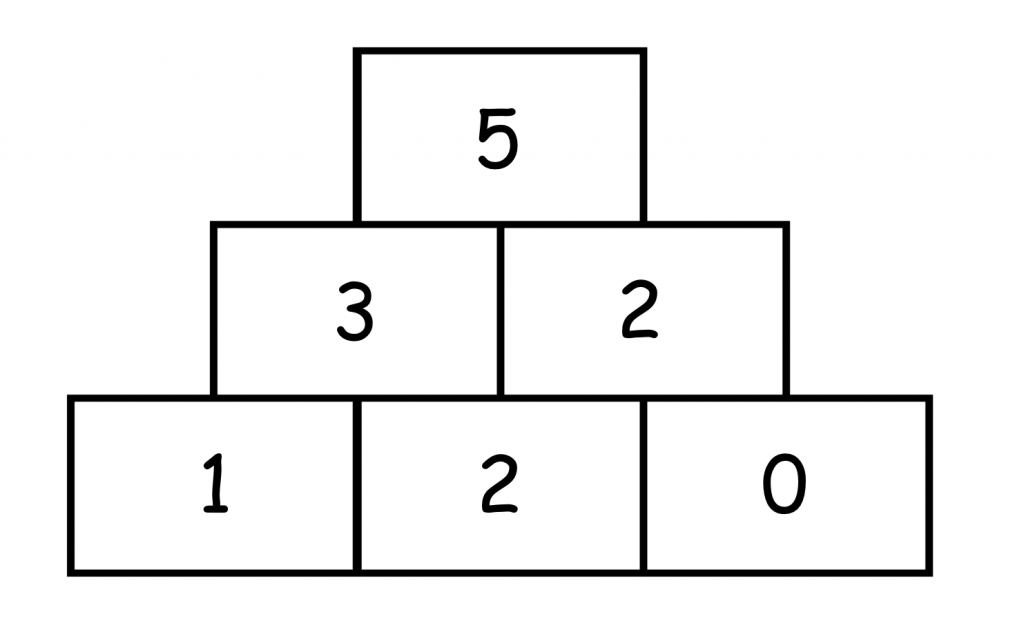
Bzw. 6, wenn die Tauschaufgaben berücksichtigt werden.
4. Reflexion
Welche Beschreibungen der Vorgehensweise sind bei Kindern zu erwarten?
Manuel begründet sehr systematisch über die Zerlegungen der Zahl 5 in zwei Summanden. So hat er aber bisher nur die Mittelsteine betrachtet.
Mias Begründung ist sehr ausführlich. Sie berücksichtigt die Zerlegungen und die Tauschaufgaben.
Eine gemeinsame Reflexion ist wichtig, für den Bewusstheitsgrad und damit die Effektivität des Lernens. Gewonnene Einsichten werden vertieft und neue Impulse im kommunikativen Austausch vermittelt. Weitere Leitfragen für den gemeinsamen Austausch über Zahlenmauern könnten beispielsweise sein:
-
Welche Mauern waren für mich besonders einfach/ schwierig und warum?
-
Wie kann man mit auftretenden Schwierigkeiten umgehen?
-
Was kann man tun, wenn man eine Mauer verändern will, der Deckstein aber gleichbleiben soll?
-
Wie kann ich leicht Zahlenmauern zu einer gegebenen Zielzahl finden?
-
usw. (Die Fragestellungen hängen auch von den tatsächlich eingesetzten Zahlenmauern bzw. Fragestellungen ab.
5. Wie kann es weitergehen?
Folgende Aufgabenvariationen von Zahlenmauern eignen sich sehr gut für ein „Zahlenmauernforscherheft“ oder für Stationen- oder Wochenplanarbeit.
Der Mittelstein einer komplett ausgefüllten 4er-Mauer (2. Zeile Mitte) soll um 1 kleiner werden, die Zielzahl aber bleiben. Wie und wo kann man ausgleichen? Begründung? Gibt es mehrere Möglichkeiten?
Ausgehend von einer vorgegeben oder erreichten Zielzahl wird eine Zielzahlveränderung gefordert (sie soll z.B. um 8 größer sein als die alte).
Durch welche Manipulation der Basissteine kann dies aus der bestehenden Mauer erreicht werden. Begründung?
Man vertausche je zwei Basiszahlen (z. B. in der 4er-Mauer: innen/innen, außen/außen, innen/außen).
Anschließend untersucht man die Wirkung dieser Handlung auf die Zielzahl. Begründung?
Bei einer 4er-Mauer ist die 2. Zeile (von unten) komplett vorgegeben. Welche Werte können die restlichen Steine tragen, wenn die beiden unteren Randsteine gleich groß sein sollen? Was fällt auf?
Insgesamt zeigt sich also, dass Zahlenmauern im Besonderen zur Förderung der allgemeinmathematischen Kompetenzen genutzt werden können. Sie „können immer wieder unter neuen Gesichtspunkten aufgegriffen werden und sind einsetzbar von Klasse 1 bis weit hinauf in die Sekundarstufe“ (Krauthausen 2016, S. 32).
Eine Forscheraufgabe
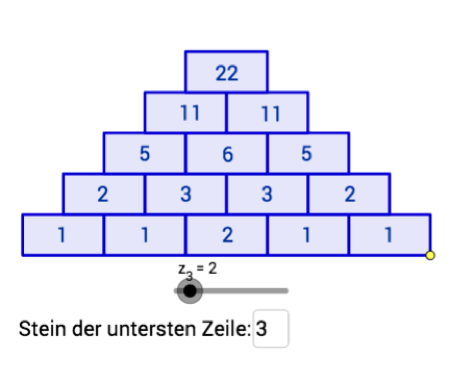
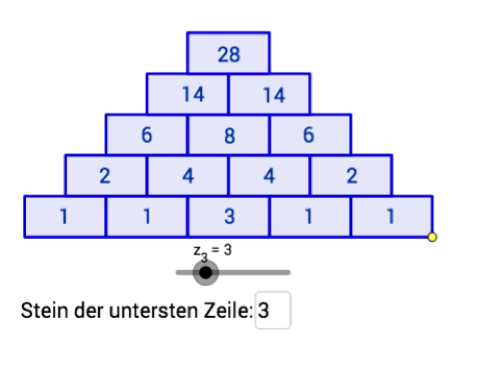
Wie verändern sich eigentlich die Werte in einer Zahlenmauer, wenn man einen Basisstein verändert? Mit der folgenden Animation können Sie dem Zusammenhang auf den Grund gehen. Wenn Sie den grauen Schieberegler bewegen, erhöht sich der erste Basisstein analog um 1. Die übrigen Steine werden automatisch berechnet. In dem Kasten können Sie eingeben, welchen der Basissteine Sie verändern möchten. Welche Auswirkungen hat die Veränderung des linken Basissteins auf den Wert im Deckstein? Wie verändert sich der Wert im Deckstein, wenn sich der mittlere Basisstein um eins erhöht? Wie lassen sich mögliche Unterschiede erklären?